Просто невозможно! (Часть 8)

Далее рассмотрим три закона механики, провозглашенные Исааком Ньютоном в 1680-х годах. Более двух столетий упорные усилия самых проницательных умов испытывали ньютоновские законы и не нашли ни одного исключения из них. Они подтверждались всевозможными экспериментами и легли в основу всей комплексной структуры механики. То, что в основных законах механики может обнаружиться какой-то значительный изъян в той области, где они так долго исследовались, в начале XX века казалось совершенно неправдоподобным.

Однако всем известно, что в 1905 году Эйнштейн пересмотрел законы механики Ньютона, представив общественности взгляд на Вселенную с точки зрения теории относительности. Однако это касалось только новейших областей знаний, не входивших в компетенцию ученых XIX и XVIII столетий. В частности, при исследовании движения на релятивистских скоростях, которые Ньютон и его последователи просто не могли исследовать, имея в распоряжении лишь инструме ... Читать дальше »

Просто невозможно! (Часть 7)

И все же, что случилось бы, если бы в каком-либо из этих случаев закон сохранения энергии был опровергнут? Что бы это значило?

Важно помнить, что наука разделяет наблюдения и теории, поэтому опровержение теории не означает опровержения наблюдений. Многим людям, далеким от науки, трудно это осознать. Раз сохранение энергии требует от нас питаться и дышать кислородом для поддержания жизни, есть туманная надежда на то, что, если бы удалось доказать ошибочность этого закона, человек вдруг перестал бы нуждаться в еде и кислороде.

Однако необходимость питания и дыхания является наблюдаемым фактом и не зависит от теорий. Если какое-либо обобщение, объясняющее необходимость, оказывается ложным, тогда нужно придумать другое обобщение для объяснения той же необходимости.

Например, на протяжении всего XIX века химики работали на основании такого фундаментального принципа, как закон сохранения массы, утверждавшего, что общая масс ... Читать дальше »

Просто невозможно! (Часть 6)

А теперь перейдем к физике. В математике человек может создать идеальный мир, соответствующий или не соответствующий реальности; такое соответствие не обязательно. Однако в физике человеком управляет четкое сознание того, что есть реальность, и тогда он может описать ее наилучшим образом.

На основании опыта (а не умозаключений, исходя из предпосылок или определений, придуманных для удобства) можно сделать определенные обобщения о материальной Вселенной. Они обычно называются «законами природы», и в этом претенциозном термине отразилась излишняя самоуверенность так называемого века разума (XIX века). На самом деле законы природы — не более чем обобщенные закономерности.

Самое мощное обобщение, которое мы знаем, может быть выражено следующими словами: общее количество энергии, присутствующей в замкнутой системе, постоянно (замкнутая система в данном случае представляет собой изолированную систему, которая не может приобрести и ... Читать дальше »

Просто невозможно! (Часть 5)

В чем же ошибка? Вернемся немного назад, к тому месту, где я сказал: «Можно разделить обе части уравнения на одно и то же число, не влияя на равенство, давайте разделим их на а — b».

Но еще раньше я говорил, что а = b, таким образом а — b равно b — b, то есть 0. Следовательно, когда я говорю: «Давайте разделим на а — b», я фактически говорю: «Давайте разделим на 0», а это в математике не разрешается.

Можете возразить: «Почему это не разрешается?»

Ответ очень прост. Если разрешить деление на 0, тогда появляется возможность доказать, что 2 = 1, как я только что продемонстрировал. Кроме того, с делением на 0 можно доказать, что лю6ое число — положительное, отрицательное, дробное, иррациональное, мнимое или трансцендентное — равно любому другому числу. Такая математическая система, в которой все числа равны, не имеет никакого смысла и математикам не нужна.

Вырабатывая правила для выполнения различных математических дейс ... Читать дальше »

Просто невозможно! (Часть 4)

Теперь посмотрим на «невозможность» другого рода. Раз уж я заговорил об ошибках, давайте разберем их подробнее. Иными словами, проанализируем цепь рассуждения, каждый шаг которого кажется абсолютно верным, но которое приводит к явно абсурдному заключению.

Для этого рассмотрим простейший известный мне алгебраический софизм; настолько простой, что даже я сумел с первого раза разглядеть его.

Возьмем для начала две равные величины, а и b:

a = b. (уравнение 1)

Обе части уравнения можно умножить на одно и то же число, не влияя на равенство; умножим обе части на а.

а² = аb. (уравнение 2)

Из обеих частей уравнения можно вычесть одно и то же число, не влияя иа равенство; вычтем  b² из обеих частей.

а² — b² = аb - b². (уравнение 3)

Выражение а² -  b² может быть получено умножением а + b на а - ... Читать дальше »

Просто невозможно! (Часть 3)

Бесполезно говорить мне: «Откуда вы знаете? Вы что, пробовали складывать и отнимать все возможные сочетания четных чисел? Может быть, есть какое-то сочетание необычных четных чисел, которое вы никогда не встречали, а оно дает при сложении нечетное число».

Отвечаю: мне не нужно пробовать все возможные сочетания четных чисел. Определения четного и нечетного числа составлены таким образом, что исключают получение нечетного числа путем сложения или вычитания четных чисел.

А если мне на это скажут: «Но я проделал очень сложную операцию по сложению двадцати разных четных чисел, и в сумме получилось нечетное число», я отвечу: вы сделали арифметическую ошибку.

Тогда мне могут пожаловаться: «Откуда вы знаете? Может, проверите?»

Наверное, я мог бы сложить эти числа сам, найти ошибку и отвязаться от этого надоеды, но я имею полное право отказаться и заявить: вы сделали арифметическую ошибку. Ищите ее сами. Я зря терять времени ... Читать дальше »

Просто невозможно! (Часть 2)

Начнем с выражения 2 + 2. 2 + 2 равно 4, не так ли? Прибавим еще 2 и получим 6, потом 8, потом 10 и так до бесконечности. Если мы начнем с 0 и будем каждый раз прибавлять по 2, то построим ряд четных чисел, а именно 2, 4, б, 8, 10, 12, 14, 16...

Вы сами интуитивно (просто взглянув на ряд чисел) понимаете, что все четные числа делятся на 2. Или, поскольку мы определили четное число как сумму 2 + 2 + 2 + 2..., можно заменить это выражение другим: 2(1 + 1 + 1 + 1...) — для суммы любого угодного вам количества двоек. Следовательно, все четные числа кратны 2.

Теперь сложим любые два четных числа: 2 + 4, или 72 + 106, или 8 640 772 + 54, или какие угодно другие четные числа. Что можно сказать об их сумме? Раз любое четное число можно записать в виде суммы двоек, то есть сложить 2 + 2 + 2 +2...и 2 + 2 + 2 + 2..., то в результате сложения обязательно получатся два ряда двоек, составленные вместе: 2 + 2 + 2 + 2...+ 2 + 2 + 2 + 2...

... Читать дальше »

Просто невозможно! (Часть 1)

Общеизвестно, что моя молодость еще не прошла, и менее всего мне хотелось бы играть роль консервативного старца — закостеневшего в старых идеях педанта.

Но порой обстоятельства вынуждают меня принимать на себя эту роль. Например, как-то раз я смотрел первую серию комедийного сериала «Время пришло». Его премьере состоялась в 1966 году, и речь в нем шла о парочке самодовольных астронавтов, которые оказываются в мифическом каменном веке, где пещерные люди говорят по-английски и дрессируют динозавров.

Пребывание астронавтов в доисторическом времени объяснялось тем, что их корабль случайно развил сверхсветовую скорость. Помню, один из них сказал другому: «Теория Эйнштейна утверждает, что если путешествовать со сверхсветовой скоростью, то время поворачивает вспять».

За кадром на эту реплику не был наложен смех, но я, естественно, расхохотался, и моя маленькая дочь, которая смотрела телевизор вместе со мной, спросила, почему я см ... Читать дальше »

Космический четырехлистник (Часть 11)

Но если все начинается с Ничего, почему оно не остается Ничем?

А почему оно должно оставаться ничем? Можно сказать, что 0 + 0 = 0 и что +1 + (-1) = 0. Оба выражения — 0 + 0и+1 + (—1) — являются эквивалентами понятия «ноль», так почему одно из них должно быть более «реальным» или «естественным», чем другое? Ничто может свободно переходить в четырехлистник, поскольку этот переход, по существу, не меняет основных положений.

Но почему изменение происходит именно в этот момент времени, а не в другой? Одно то, что изменение происходит в конкретный момент времени, означает, что нечто явилось его причиной.

Неужели? Но что вы подразумеваете под моментом времени? Время и пространство существуют лишь в соединении с расширением и сжатием лепестков четырехлистника. Когда лепестков не существует, не существует ни времени, ни пространства.

В Начале не было Ничего — ни времени, ни пространства.

Четырехлистник появля ... Читать дальше »

Космический четырехлистник (Часть 10)

По мере расширения космона и отрицательного космона гравитационное отталкивание неуклонно разводит их прочь друг от друга по шкале пространства (см. рис. 1) при движении по временной шкале. Подобным образом антикосмон и отрицательный антикосмон неуклонно расходятся врозь по пространственной шкале, хотя двигаются вместе вниз по временной шкале.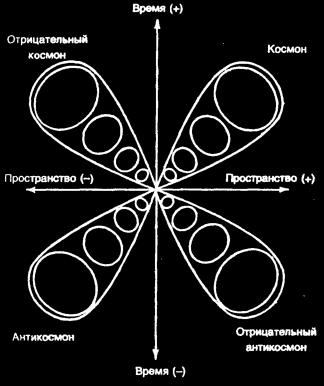


Как показывает рис. 1, в результате возникает картина, очень похожая на четырехлистный клевер (который вынесен в название главы, если им еще не догадались).

Как только различные Вселенные проходят пик своего расширения и снова начинают сжиматься, вспять, возможно, поворачивает не только время, по и эффект гравитации. Некоторые знаменитые физики выдвигают теории, утверждающи ... Читать дальше »