§ 57. Открытие Нептуна

Одним из самых блестящих достижений небесной механики является открытие планеты Нептун.

В 1781 г. английский астроном Уильям Гершель открыл новую большую планету, получившую название Уран, которую раньше принимали за звезду и неоднократно, почти в течение целого столетия, определяли ее координаты. Когда по этим координатам стали вычислять орбиту Урана, то оказалось, что в его движении, даже после учета всех возмущений от известных тогда больших планет, имеются отклонения от кеплеровского движения. Для объяснения этих остаточных отклонений было сделано предположение, что они вызываются действием еще одной неизвестной планеты, и перед астрономией возникла задача: по возмущениям в движении Урана определить положение (координаты) возмущающей планеты. Эта трудная математическая задача была решена почти одновременно, независимо друг от друга, французским ученым Леверрье и английским — Адамсом. 23 сентября 1846 г. немецкий астроном Галле нашел предп ... Читать дальше »

§ 56. Задача трех и более тел 

Определение движения трех тел, взаимно притягивающих друг друга с силой, обратно пропорциональной квадрату расстояния между ними, называется задачей трех тел.

В 1912 г. финский математик Зундман получил теоретическое решение этой задачи при произвольных начальных условиях в виде сходящихся рядов. Но эти ряды настолько сложны и сходятся так медленно, что не позволяют ни вычислять положения тел в пространстве, ни делать какие-либо заключения о характере и свойствах движений тел. Поэтому формулы Зундмана практического значения пока не имеют.

Лагранж в 1772 г. доказал, что существует определенное количество частных случаев в задаче о трех телах, в которых может быть найдено точное решение. Если заданы массы тел и их положение на плоскости, как, например, на рис. 206 из § 156, то рассматриваемые частные случаи движения в этой плоскости получаются при расположении третьего тела в одной из пяти точек, называемых то ... Читать дальше »

§ 55. Приливы и отливы 

Так как размеры Земли не бесконечно малы по сравнению с расстояниями до Луны и Солнца, то, независимо от формы Земли, силы лунного и солнечного притяжения на разные точки Земли неодинаковы. В результате появляется возмущающая сила, действующая на эти точки сообразно различным расстояниям и направлениям от этих точек до притягивающего тела. Если бы Земля была абсолютно твердым телом, т.е. ее точки не могли бы изменять своего положения относительно центра Земли, то под действием этих возмущающих сил в теле Земли появились бы только едва заметные натяжения. Но Земля не абсолютно твердое тело, поэтому действие возмущающих сил на некоторые части земной поверхности вызывает явления, которые называются приливами и отливами.

Допустим для простоты, что твердая поверхность Земли со всех сторон равномерно покрыта океаном (рис. 34). Луна притягивает к себе каждую частицу твердой поверхности Земли и каждую каплю воды в океане, сообщая ... Читать дальше »

§ 54. Сила, возмущающая движение Луны 

Для Луны центральным телом является Земля, а основным возмущающим телом — Солнце.

Притяжения планет также влияют на движение Луны, но вызываемые ими возмущения сравнительно невелики и во много раз меньше возмущений, вызываемых Солнцем. Притяжение Солнца сообщает Луне ускорение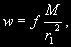

где М — масса Солнца, a r1 — расстояние Луны от Солнца.

Земля же притягивает Луну с силой, сообщающей Луне ускорение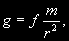

где т — масса Земли, а r — расстояние Луны от Земли. Разделив первое ускорение на второе, получим
... Читать дальше »

§ 53. Понятие о возмущающей силе 

Пусть имеются три небесных тела: Солнце С с массой М, планета P1 с массой m1 на расстоянии r1 от центра Солнца и планета Р2 с массой т2 на расстоянии r2 от центра Солнца и на расстоянии r от планеты Р1 (рис. 32). Все три тела действуют друг на друга по закону всемирного тяготения Ньютона.

Солнце получает ускорение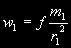

по направлению СР2 от планеты P1 и ускорение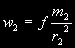

по направлению СР2 от планеты Р2 .

Рассмотрим движение планеты P1 относительно Солнца. В этом случае на планету P1 будут действова ... Читать дальше »

§ 52. Понятие о возмущенном движении 

Если бы какое-нибудь тело Солнечной системы притягивалось только Солнцем, то оно двигалось бы вокруг Солнца точно по законам Кеплера. Такое движение, соответствующее решению задачи двух тел, называют невозмущенным. В действительности же все тела Солнечной системы притягиваются не только Солнцем, но и друг другом. Поэтому ни одно тело в Солнечной системе не может точно двигаться по эллипсу, параболе, гиперболе и тем более по кругу. Отклонения в движениях тел от законов Кеплера называются возмущениями, а реальное движение тел — возмущенным движением. Возмущения тел Солнечной системы имеют очень сложный характер, и их учет чрезвычайно труден, хотя они сравнительно и невелики, так как массы этих тел по сравнению с массой Солнца очень малы (общая их масса меньше 1/700 массы Солнца). Возмущения можно рассматривать как различие между положениями светила при возмущенном и невозмущенном движениях, а ... Читать дальше »

§ 51. Третий (уточненный) закон Кеплера 

При круговом движении ускорение w = w2r, где угловая скорость 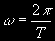, а Т — период обращения по окружности. Следовательно, ускорение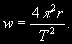

Если рассматривать относительное движение по кругу небесного тела с массой т вокруг центрального тела с массой M, то согласно уравнению (2.17) относительное ускорение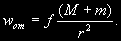

Так как w и wот — одно и то же ускорение, то, приравняв их правые части, получим
... Читать дальше »

§ 50. Второй закон Кеплера 

Возьмем прямоугольную систему координат, начало которой находится в центре притяжения, а плоскость ху совпадает с плоскостью орбиты тела.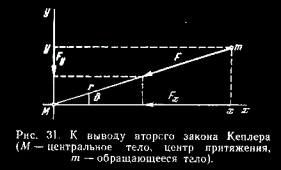
  
Проектируя ускорение и силу на координатные оси х и у (рис. 31), напишем основное уравнение динамики (2.14) в следующем виде: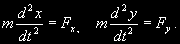

Умножая эти уравнения соответственно на у и х и вычитая первое из второго, получим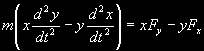

или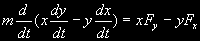
... Читать дальше »

§ 49. Первый (обобщенный) закон Кеплера 

Законы Кеплера были получены им эмпирически в результате исследования видимых движений планет. Поэтому первый закон Кеплера в формулировке, данной в § 40, справедлив лишь в отношении больших планет и тех тел Солнечной системы (некоторых комет, астероидов), которые движутся вокруг Солнца по замкнутым орбитам.

Если же иметь в виду движения небесных тел вообще, то на основании предыдущего параграфа этот закон надо сформулировать в следующем виде: под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе.

В этой формулировке первый закон Кеплера будет справедлив уже для всех комет, орбиты которых либо эллипсы, либо параболы, либо гиперболы; он будет справедлив и для спутников больших планет, орбиты которых эллипсы, но в их фокусах находятся большие планеты, и для физических двойных звезд (см.&nbs ... Читать дальше »

§ 48. Движение материальной точки под действием силы притяжения (задача двух тел) 

Эта задача решается путем интегрирования дифференциальных уравнений движения, получаемых из основного уравнения динамики материальной точки (2.14), в котором силаF есть сила притяжения. Мы не будем интегрировать эти уравнения, так как с этим учащийся познакомится в курсах теоретической астрономии и небесной механики Остановимся лишь на результатах решений.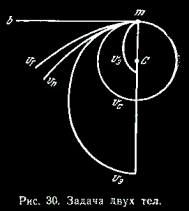
  
Если неподвижная масса М, сосредоточенная в точке С, стала притягивать к себе в некоторый момент материальную точку т с силой, обратно пропорциональной квадрату расстояния, то ускорение точки т будет направлено по прямой тС, а ее дальнейшее движение будет зависеть от расстояния и от величины и направления скорости  ... Читать дальше »