§ 48. Движение материальной точки под действием силы притяжения (задача двух тел)
Эта задача решается путем интегрирования дифференциальных уравнений движения, получаемых из основного уравнения динамики материальной точки (2.14), в котором силаF есть сила притяжения. Мы не будем интегрировать эти уравнения, так как с этим учащийся познакомится в курсах теоретической астрономии и небесной механики Остановимся лишь на результатах решений.
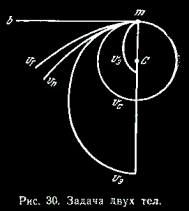
Если неподвижная масса М, сосредоточенная в точке С, стала притягивать к себе в некоторый момент материальную точку т с силой, обратно пропорциональной квадрату расстояния, то ускорение точки т будет направлено по прямой тС, а ее дальнейшее движение будет зависеть от расстояния и от величины и направления скорости v0, которые она имела в начальный момент (в момент начала действия притяжения массой М).
Если скорость v0 > 0, но не превосходит некоторого предела vc , то точка т будет двигаться по эллипсу, в одном из фокусов которого будет находиться точка С (рис. 30). Плоскость эллипса будет проходить через точки С, т и направление скорости v0 .
Форма и размеры эллипса будут различны, смотря по величине скорости v0 . При малых v0 эллипс будет сильно сжатым, его большая ось будет лишь немного больше, чем Cm, иточка С будет находиться в фокусе, далеком от m. Если скорость v0 будет близка к скорости vc , но меньше ее, то эксцентриситет эллипса будет мал, его большая полуось будет лишь немного меньше, чем Cm, точка С приблизится к центру эллипса, но останется в фокусе, далеком от т.
Если начальная скорость v0 = vc и будет направлена перпендикулярно к линии Cm, то точка m будет двигаться по кругу радиуса Сm.
Если v0 > vc , но не превосходит некоторого предела vп = vc 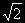 , то точка т будет двигаться по эллипсу, но точка С при этом будет находиться в фокусе, близком к m, а большая ось эллипса будет тем больше, чем ближе v0 к vп . , то точка т будет двигаться по эллипсу, но точка С при этом будет находиться в фокусе, близком к m, а большая ось эллипса будет тем больше, чем ближе v0 к vп .
Если v0 = vп = vc 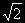 , то точка т будет двигаться по параболе, обе ветви которой уходят в бесконечность, приближаясь к направлению, параллельному оси Ст. По мере того как точка т будет удаляться от тела М, ее скорость будет стремиться к нулю. , то точка т будет двигаться по параболе, обе ветви которой уходят в бесконечность, приближаясь к направлению, параллельному оси Ст. По мере того как точка т будет удаляться от тела М, ее скорость будет стремиться к нулю.
Если v0 > vп , то точка т будет двигаться по гиперболе, ветви которой уходят в бесконечность и, при очень большой начальной скорости, приближаются к направлению, перпендикулярному к оси Ст. По мере того как точка т будет удаляться по гиперболе, ее скорость будет стремиться к некоторой постоянной величине.
Наконец, в предельных случаях, когда v0 = ¥, точка т будет двигаться по прямой тb, а когда v0 = 0, то по прямой тС.
Скорость v точки т на любом расстоянии r от точки С получается из формулы
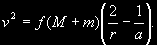 (2.18) (2.18)
где а — большая полуось эллипса. Эта формула называется интегралом энергии.
Если точка m движется по кругу, т.е. r = а, то из уравнения (2.18) следует
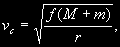 (2.19) (2.19)
а если точка m движется по параболе, то а = ¥ и
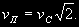 (2.20) (2.20)
Скорость vc называется круговой скоростью, а vп — параболической скоростью. Скорость эллиптического движения vэ заключена в пределах 0 < vэ < vп , а гиперболическая скорость vr > vп . Гиперболическая орбита определяется теми же шестью элементами, что и эллиптическая (см. § 41), только вместо большой полуоси а = ¥ дается перигельное расстояние q. Параболическая орбита определяется пятью элементами: i, <, w, t0 и q, так как для параболы а = ¥ и е = 1.
|

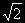 , то точка т будет двигаться по эллипсу, но точка С при этом будет находиться в фокусе, близком к m, а большая ось эллипса будет тем больше, чем ближе v0 к vп .
, то точка т будет двигаться по эллипсу, но точка С при этом будет находиться в фокусе, близком к m, а большая ось эллипса будет тем больше, чем ближе v0 к vп .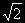 , то точка т будет двигаться по параболе, обе ветви которой уходят в бесконечность, приближаясь к направлению, параллельному оси Ст. По мере того как точка т будет удаляться от тела М, ее скорость будет стремиться к нулю.
, то точка т будет двигаться по параболе, обе ветви которой уходят в бесконечность, приближаясь к направлению, параллельному оси Ст. По мере того как точка т будет удаляться от тела М, ее скорость будет стремиться к нулю.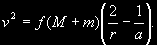 (2.18)
(2.18)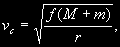 (2.19)
(2.19)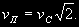 (2.20)
(2.20)




