§ 67. Определение размеров и формы светил 

Угол, под которым с Земли виден диск светила, называется его угловым диаметром. Угловые диаметры некоторых небесных тел (Солнца, Луны, планет) можно определить непосредственно из наблюдений.

Если известен угловой диаметр (или радиус) светила и его расстояние от Земли, то легко вычислить его истинный диаметр (или радиус) в линейных  мерах.  Действительно, если (рис. 44) r — угловой радиус светила М,  D — расстояние между центрами светила и Земли, р0 — горизонтальный экваториальный параллакс светила, а R0 и r — линейные радиусы Земли Т и светила М, то r = D sin r, a R0  = D sin p0 , откуда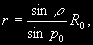
 &nb ... Читать дальше »

§ 66. Определение астрономической единицы (параллакса Солнца)         

Если известны радиус Земли R и горизонтальный параллакс Солнца р¤, то по формуле (3.2) легко вычислить среднее расстояние Земли от Солнца, т. е. значение астрономической единицы в километрах. Точность определения астрономической единицы почти целиком зависит от точности горизонтального параллакса Солнца р¤. Однако непосредственное определение горизонтального параллакса Солнца способом, описанным в предыдущем параграфе, дает слишком грубые результаты вследствие удаленности Солнца и больших ошибок наблюдений, возникающих от нагревания инструмента солнечными лучами. Поэтому точное значение горизонтального параллакса Солнца определяется косвенным путем, по измеренному горизонтальному параллаксу планеты, которая подходит к Земле на расстояние меньшее, чем расстояние Земли от Солнца, и наблюдение которой удобно производить.

До& ... Читать дальше »

§ 65. Определение суточного и годичного параллаксов из наблюдений 

Пусть из двух точек O1 и О2 (рис. 42) на поверхности Земли, лежащих на одном географическом меридиане, измерены зенитные расстояния z1 и z2 одного и того же светила М в момент прохождения его через небесный меридиан. Предположим далее, что оба пункта наблюдения находятся в северном полушарии и светило наблюдалось в каждом из них к югу от зенита.

Следовательно,
z1  =  j 1 — d 1     и     z2 = j 2 — d 2,где j 1 и j 2 — географические широты пунктов, a d 1 и d 2 — топоцентрические склонения светила, отличающиеся от его геоцентрического склонения d  на величины (см. § 31)
... Читать дальше »

§ 64. Единицы расстояний в астрономии 

Если расстояния до небесных тел очень велики, то выражать их в километрах неудобно, так как получаются очень большие числа, состоящие из многих цифр.

Поэтому в астрономии, помимо километров, приняты следующие единицы расстояний:
астрономическая единица (а.е.) — среднее расстояние Земли от Солнца;
парсек (пс) — расстояние, соответствующее годичному параллаксу в 1";
световой год — расстояние, которое свет проходит за один год, распространяясь со скоростью около 300 000 км/сек. Если астрономическую единицу принять равной 149 600 000км (см. § 66), то 1 пс = 30,86×1012 км  = 206 265 а.е. = 3,26 светового года; 1 световой год = 9,460×1012 км = 63 240 а.е. = 0,3067 пс.

В астрономических единицах обычно выражаются расстоянии до тел Солнечной системы. Например, Меркурий находится от Солнца на расстоянии 0,387 а.е., а Плут ... Читать дальше »

§ 63. Определение расстояний до небесных тел 

Определение расстояний до тел Солнечной системы основано на измерении их горизонтальных параллаксов, рассмотренных в § 31.

Зная горизонтальный экваториальный параллакс р0 светила, легко определить его расстояние от центра Земли (см. рис. 20). Действительно, если ТО = R0 есть экваториальный радиус Земли, ТМ = D — расстояние от центра Земли до светила М, а угол р — горизонтальный экваториальный параллакс светила р0 , то из прямоугольного треугольника ТОМимеем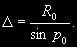
(3.1)
Для всех светил, кроме Луны, параллаксы очень малы. Поэтому формулу (3.1) можно написать иначе, положив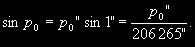
... Читать дальше »

§ 62. Размеры и форма Земли 

Метод триангуляции впервые был применен Снеллиусом в 1615 г. при измерении дуги меридиана в Голландии. С тех пор и до настоящего времени в разных странах, на разных широтах было измерено много дуг на поверхности Земли и не только по меридианам, но и по параллелям. Все эти измерения показали, что длина дуги 1° меридиана не одинакова под разными широтами: около экватора она равна 110,6 км, а около полюсов — 111,7 км, т.е. увеличивается к полюсам. Это означает, что кривизна земной поверхности меньше в полярных областях, чем в экваториальных. Следовательно, Земля отличается от шара и имеет несколько сплющенную форму, близкую к сфероиду (эллипсоиду вращения).

На протяжении последних полутора столетий неоднократно определялись элементы земного сфероида, форма которого наилучшим образом согласовывалась с наиболее точными измерениями дуг. Фундаментальные определения были сделаны в СССР Ф.Н. Красовским и А.А. Изотовым в ... Читать дальше »

§ 61. Определение радиуса Земли. Триангуляция 

Согласно теории всемирного тяготения всякое массивное, изолированное тело, вращающееся вокруг оси с определенной скоростью (не очень быстро), должно принять форму, близкую к шару. Действительно, все наблюдаемые массивные небесные тела (Солнце, Луна, планеты) имеют формы, мало отличающиеся от правильных шаров. Шарообразность Земли хорошо видна на ее фотографиях, полученных из космоса (1967-1969 гг.).
  
Шарообразность Земли позволяет определить ее размеры способом, который был впервые применен еще Эратосфеном в III в. до н. э. Идея этого способа проста. Возьмем на земном шаре две точки O1 и О2 , лежащие на одном географическом меридиане (рис. 38). Обозначим длину дуги меридиана O1O2 (например, в километрах) че ... Читать дальше »

§ 60. Движение космических аппаратов 

Траектория космического аппарата состоит из двух основных участков: активного и пассивного. Движение на активном участке определяется в основном тягой реактивных двигателей и притяжением Земли. Пассивный участок траектории начинается с момента выключения двигателя последней ступени. На пассивном участке космический аппарат движется под действием притяжения Земли и других тел Солнечной системы (Луны, Солнца, планет).

При предварительном расчете космических траекторий пользуются приближенной методикой, которая заключается в следующем. Если скорость аппарата в начале пассивного участка равна (или больше) параболической скорости (2.20) относительно Земли, то, если пренебречь возмущениями, космический аппарат будет двигаться относительно Земли по параболе (или по гиперболе) до тех пор, пока он не выйдет из сферы действия Земли или не войдет в сферу действия другого небесного тела.

Сферой действия какого-либо тела с массо ... Читать дальше »

§ 59. Движение искусственных спутников Земли 

Запуском 4 октября 1957 г. первого в мире советского искусственного спутника Земли человечество открыло новую эру в своей истории — эру создания искусственных небесных тел.

Хотя искусственные небесные тела подчиняются тем же законам, что и естественные, некоторые особенности их орбит и условия, определяющие характер их движения, заслуживают отдельного рассмотрения.

Искусственные спутники Земли (ИСЗ) выводятся на орбиту с помощью многоступенчатых ракет. Последняя ступень ракеты сообщает спутнику определенную скорость на заданной высоте. Тело, запущенное горизонтально на высоте h от поверхности Земли, станет ИСЗ, если его скорость в этот момент окажется достаточной.

Если скорость запуска точно равна круговой скорости на данной высоте h, то тело будет двигаться по круговой орбите.

Если эта скорость превышает круговую, то тело будет двигаться по эллипсу, причем перигей этого элл ... Читать дальше »

§ 58. Определение масс небесных тел 

 Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу. 

 Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.

Первый способ применим пока только к Земле и заключается в следующем.

На основании закона тяготения ускорение силы тяжести на поверхности Земли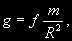

где т — масса Земли, a R — ее радиус. Отсюда масса Земли 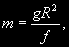( ... Читать дальше »