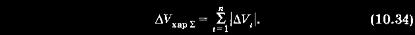10.3. Общий подход к решению задан оптимизации управления маневрами околокруговых КА
В отличие от приведенной выше упрощенной постановки задачи минимизации энергетических затрат на импульсное изменение элементов орбиты, здесь, ориентируясь на результаты работы [16], дадим ее обобщение для случая, более полно отражающего реальную ситуацию.
Ниш, пусть заданы граничные условия в виде параметров начальной и конечной орбит для рассматриваемой модели движения при фиксированных ограничениях. В виде таких ограничений могут выступать параметры переходной орбиты, моменты формирования импульсов, их величина и т. д.
Необходимо путем выдачи п управляющих импульсов скорости, формируемых КДУ на витках N1 N2, ..., Nn, получить на заданном витке с номером N3 желаемые значения параметров орбиты q1, ..., qm, минимизировав суммарные энергетические затраты:
В изложенной постановке обсуждаемую задачу относят к классу задач условной оптимизации.
К числу важнейших этапов решения таких задач относят анализ физической сущности и принимаемых во внимание особенностей маневрирования при разработке упрощенной модели движения, допускающей возможность поиска начального приближения и расчета частных производных для градиентных методов уточнения.
Самым используемым подходом, применяемым при упрощении математической модели маневра, является подход, базирующийся на линеаризации в окрестности номинального движения изменяемого параметра орбиты (как правило, круговой) по величинам импульсов скорости, направленных по трансверсали в плоскости орбиты.
Обычно принимают допущение, что величины формируемых импульсов существенно меньше орбитальной (круговой) скорости.
Пусть q0 — номинальное значение изменяемого параметра; qтр — требуемое значение, полученное в результате приложения л импульсов. Очевидно, что величина изменяемого параметра должна быть функцией параметров управления, в качестве которых выступают величина и аргумент широты точки приложения ui i-го импульса:
|