§ 97. Меридианный круг 

Меридианный круг (рис. 74) состоит из астрономической трубы АВ, которая может вращаться только вокруг горизонтальной оси EW. Последняя лежит на прямоугольных вырезах (лагерах), прикрепленных к кирпичным или каменным столбам, установленным на солидном фундаменте. Горизонтальная ось меридианного круга должна быть направлена точно с востока на запад. Тогда труба будет располагаться и вращаться точно в плоскости небесного меридиана.

На горизонтальную ось EW наглухо насажен круг CD (или два круга), вращающийся вместе с трубой АВ. На круге с очень большой точностью нанесены штрихи через каждые 2' или 4'. Отсчеты на круге производятся по неподвижному указателю М, укрепленному на столбе. Увеличение точности отсчета достигается с помощью микроскопа с измерительным приспособлением — микрометром, установленным рядом с неподвижным указателем. Микроскоп-микрометр позволяет измерять рас ... Читать дальше »

§ 96. Секстант 

При наблюдениях на море (с палубы корабля) или в воздухе (с борта самолета) пользуются переносным инструментом, называемым секстантом. Он не требует прочной установки, и при наблюдениях его держат в руках. Существенной особенностью этого инструмента является то, что визирование обоих предметов, между которыми измеряется угол, осуществляется не последовательно, а одновременно и заключается в совмещении изображений обеих наблюдаемых точек в поле зрения трубы.

Секстант (рис. 72) состоит из металлической рамы с лимбом LL', представляющим часть окружности, немногим более 60° ; алидады a ,  вращающейся вокруг оси, проходящей через 

§ 95. Универсальный инструмент 

Одним из основных угломерных инструментов, позволяющим в любой точке земной поверхности измерить горизонтальные координаты светила, является универсальный инструмент (рис. 70), который состоит из небольшой астрономической трубы, имеющей возможность поворачиваться вокруг двух взаимно перпендикулярных   осей —горизонтальной   и   вертикальной. Установка осей в плоскости математического горизонта и в вертикальной плоскости производится с помощью уровней и регулировочных винтов.
  
Углы поворота трубы около той и другой оси отсчитываются по двум кругам или лимбам — вертикальному и горизонтальному. Вертикальный круг соединен с горизонтальной осью и служит для отсчетов углов в вертикальной плоскости; ... Читать дальше »

§ 94. Угломерные инструменты. Астрономическая труба 

Из принципов решения астрономических задач следует, что во время наблюдений необходимо измерять углы в горизонтальной и вертикальной плоскостях и отмечать моменты времени.

Измерение углов производится угломерными инструментами различных конструкций. Современные астрономические угломерные инструменты являются довольно сложными, прецизионными приборами. Здесь нет необходимости входить в технические детали и рассматривать все многочисленные конструкции угломерных инструментов. Поэтому в дальнейшем мы ограничимся только кратким описанием главнейших из них и рассмотрим лишь основные идеи их устройства.

Основными частями угломерного инструмента являются точно разделенные круги и астрономическая труба, играющая роль визира.

Астрономическая труба в принципе состоит из тубуса и двух двояковыпуклых собирающих линз, помещенных на ее концах. Одна из линз, обращенная к рассматриваемому объекту, называется&n ... Читать дальше »

§ 93. Астрономические каталоги и звездные карты 

Экваториальные координаты светил, полученные непосредственно из наблюдений и исправленные за рефракцию (см. § 30), называются видимыми. Если из видимых координат исключить влияние аберрации света (см. § 69), то получим истинные координаты. И наконец, если из истинных координат исключить влияние нутации (см. § 72), то получим средниеэкваториальные координаты светила в момент наблюдения. Средние экваториальные координаты светила можно вычислить и для любого другого момента, если учесть влияние прецессии (см. § 72).

Средние экваториальные координаты звезд, отнесенные к началу какого-нибудь года, заносятся в списки, которые называются каталогами положений или звездными каталогами.Начало года, для которого даны средние координаты звезд, называется равноденствием каталога. Каталоги положений делятся на абсолютные (полученные из абсолютных ... Читать дальше »

§ 92. Фотографическая астрометрия 

Для исследования строения и развития Вселенной, и в первую очередь Галактики, необходимо знать положения (координаты и расстояния) и движения как можно большего числа объектов (в идеале всех), входящих в ее состав.

Визуальные методы астрометрии позволяют получить координаты и собственные движения только для сравнительно ярких объектов, а расстояние — для объектов сравнительно близких (см. § 65). Получение этих характеристик для слабых и удаленных объектов до середины XIX в. практически было невозможно,

Применение фотографии в астрономии вызвало развитие фотографических методов почти во всех ее разделах, в том числе и в астрометрии.

Фотографический метод наблюдений для астрометрии ценен тем, что: 1) ему доступны объекты более слабые, чем наблюдаемые визуально; 2) на одном астронегативе одновременно получаются изображения большого числа звезд (до нескольких тысяч) и других небесных объектов, среди к ... Читать дальше »

§ 91. Собственные движения звезд 

Из сравнения экваториальных координат одних и тех же звезд, определенных через значительные промежутки времени, было обнаружено, что их прямые восхождения и склонения меняются с течением времени. Значительная часть этих изменений вызывается прецессией, нутацией, аберрацией и, в меньшей степени, годичным параллаксом (см. §§ 63, 69, 73). Если исключить влияние этих причин, то изменения уменьшаются, но не исчезают полностью. Оставшееся смещение звезды на небесной сфере за год называетсясобственным движением звезды m . Оно выражается в секундах дуги в год.

Собственные движения у разных звезд различны по величине и направлению. Только несколько десятков звезд имеют собственные движения больше 1" в год. Самое большое известное собственное движение m  = 10”,27 (у "летящей” звезды Барнарда). Громадное же большинство измеренных собственных движений у звезд составляют сотые и тысячные доли секунды ... Читать дальше »

§ 90. Абсолютные и относительные методы определения экваториальных координат (a  и d  ) 

Экваториальные координаты светил могут быть определены либо абсолютным методом, либо относительным пли дифференциальным методом.

Определение координат абсолютным методом не опирается на какие-либо заранее известные координаты. При дифференциальном же методе прямые восхождения и склонения нескольких десятков или сотен звезд должны быть заранее известны. Эти звезды называются опорными.

а) Абсолютные методы. Определение склонений звезд абсолютным методом основано на соображениях и формулах § 14. Действительно, если измерить зенитное расстояние незаходящсй звезды сначала в момент ее верхней кульминации (zB ), о затем, через 12 часов звездного времени, в момент ее нижней кульминации (zH ), то будем иметь (см. формулы§ 14)
zB  = d   — j 
и
zH  = ... Читать дальше »

§ 89. Задачи фундаментальной астрометрии 

Фундаментальная астрометрия — учение об инерциальных системах отсчета в астрономии, т.е. о системах, обладающих только прямолинейным и равномерным движением без вращения. Основу для создания таких систем дает нам построение на небесной сфере системы координат и собственных движений звезд и установление системы фундаментальных постоянных астрономии — величин, позволяющих учитывать закономерные изменения координат со временем. Отсюда следуют две основные задачи фундаментальной астрометрии: 1) определение координат и собственных движений звезд; 2) определение числовых значений фундаментальных астрономических постоянных. Принципы определения некоторых основных постоянных астрономии (прецессии, нутации, аберрации, параллакса Солнца) ясны из описания этих явлений, данных ранее в соответствующих параграфах. Поэтому в следующих параграфах мы ограничимся рассмотрением лишь первой задачи — определением координат и собственных движений ... Читать дальше »

§ 88. Определение азимута земного предмета 

Определение азимута направления на земной премет П состоит из определения астрономического азимута А какого-либо светила M и из измерения горизонтального угла DAмежду вертикальными кругами светила и земного предмета (рис. 66). Тогда азимут земного предмета AП получим из уравнения
AП  = A —  DA.(6.12)
Об измерении разности азимутов двух предметов, т.е. угла DА, сказано в § 95. 
 
Астрономический азимут светила A можно вычислить по двум формулам. Одна из них получается из первой формулы (1.36):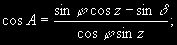

здесь достаточно измерить ... Читать дальше »