§ 90. Абсолютные и относительные методы определения экваториальных координат (a и d )
Экваториальные координаты светил могут быть определены либо абсолютным методом, либо относительным пли дифференциальным методом.
Определение координат абсолютным методом не опирается на какие-либо заранее известные координаты. При дифференциальном же методе прямые восхождения и склонения нескольких десятков или сотен звезд должны быть заранее известны. Эти звезды называются опорными.
а) Абсолютные методы. Определение склонений звезд абсолютным методом основано на соображениях и формулах § 14. Действительно, если измерить зенитное расстояние незаходящсй звезды сначала в момент ее верхней кульминации (zB ), о затем, через 12 часов звездного времени, в момент ее нижней кульминации (zH ), то будем иметь (см. формулы§ 14)
zB = d — j
и
zH = 180° — j — d ,
откуда
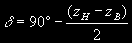
Таким образом, не зная координат других светил, мы получим склонение d данной звезды и географическую широту j места наблюдения.
После того как широта места j будет многократно определена из наблюдений нескольких незаходящих звезд, взяв среднее арифметическое ее значение j 0 и измерив зенитное расстояние уже любой звезды в момент кульминации, получим склонение звезды по одной из следующих формул:
d = j 0 — z, если звезда кульминировала к югу от зенита;
d = j 0 + z, eсли звезда кульминировала к северу от зенита;
d = 180 ° — j — z, если звезда наблюдалась в нижней кульминации.
Абсолютный метол определения прямых восхождений основан на том соображении, что из наблюдений Солнца можно найти его прямое восхождение a ¤, не зная прямых восхождений других светил.
Действительно, пусть на рис. 67 QQ' — небесный экватор, EE' — эклиптика, A — точка весеннего равноденствия, e — наклонение небесного экватора к эклиптике, а С —положение Солнца на эклиптике в некоторый момент. Тогда дуга Cm — склонение d ¤ Солнца, а дуга Am — его прямое восхождение a ¤.
|