Зеркальная симметрия
Создав общую теорию относительности, Эйнштейн связал физику
тяготения с геометрией пространства‑времени. На первый взгляд, теория струн
укрепляет и расширяет связь между физикой и геометрией: свойства колеблющихся
струн (например, массы и переносимые ими заряды) в значительной степени
определяются свойствами свернутой компоненты пространства. Однако, как мы
только что видели, квантовая геометрия, связывающая геометрические и физические
стороны теории струн, обладает рядом удивительных свойств. В общей теории
относительности, как и в «традиционной» геометрии, окружность радиуса R
отличается от окружности радиуса \/R, что кажется незыблемым и очевидным, а в
теории струн эти окружности физически неразличимы. Этот факт подталкивает нас
пойти дальше и задаться вопросом, не существует ли геометрических структур
пространства, отличающихся друг от друга еще сильнее (не только размером, но,
возможно, и видом), но, тем не менее, физически неразличимых в теории струн?
В 1988 г. Ленc Диксон из Стэндфордского центра линейных
ускорителей сделал важнейшее в этом отношении наблюдение, которое впоследствии
было обобщено Вольфгангом Лерхе из ЦЕРНа, Вафой из Гарварда и Николасом
Уорнером, работавшим в то время в Массачусетском технологическом институте. На
основе эстетических соображений, основанных на понятии симметрии, эти физики
выдвинули смелое предположение, что два различных многообразия Калаби‑Яу,
выбранные в качестве дополнительных измерений в теории струн, могут приводить к
одинаковым физическим результатам.
Чтобы дать представление о том, как может оказаться
справедливой подобная кажущаяся невероятной гипотеза, вспомним, что число
отверстий в добавочных измерениях Калаби‑Яу определяет число семейств, в
которые группируются возбуждения струны. Эти отверстия аналогичны отверстиям
тора или его обобщений с несколькими ручками (рис. 9.1). К несчастью, на
двумерном рисунке, который можно воспроизвести на странице, нельзя
продемонстрировать то, что отверстия в шестимерном пространстве Калаби‑Яу могут
иметь различные размерности. Хотя такие отверстия трудно вообразить, их можно
описать на понятном математическом языке. Суть состоит в том, что число
семейств частиц, возникающих при возбуждениях струны, зависит только от числа
всех отверстий, а не от числа отверстий каждой конкретной размерности (вот
почему мы не заботились о том, чтобы изобразить разнообразные отверстия в главе
9). Предположим теперь, что у двух пространств Калаби‑Яу число отверстий разных
размерностей различно, но суммарное число отверстий одинаково. Так как число
отверстий различных размерностей не совпадает, два этих пространства различны.
Но так как суммарное число отверстий одинаково, число семейств в каждой
Вселенной одно и то же. Конечно, это говорит о совпадении лишь одного
физического свойства. Эквивалентность всех физических свойств — гораздо более
сильное требование, но и совпадение одного свойства уже свидетельствует в
пользу того, что гипотеза Диксона‑Лерхе‑Вафы— Уорнера может оказаться верной.
В конце 1987 г. я поступил на стажировку на физический факультет
Гарвардского университета, где мне выделили кабинет по соседству с кабинетом
Вафы. Так как тема моей диссертации была посвящена физическим и математическим
свойствам свернутых измерений Калаби‑Яу в теории струн, Вафа держал меня в
курсе своих работ в этой области. Когда в конце 1988 г. он, стоя на пороге
моего кабинета, сообщил о гипотезе, к которой они пришли совместно с Лерхе и
Уорнером, я был весьма заинтересован, но отнесся к ней скептически. Интерес
объяснялся тем, что в случае, если гипотеза окажется верной, она может открыть
новые просторы исследований в теории струн, а скепсис был следствием понимания
того, что догадки и установленные свойства теории — далеко не одно и то же.
На протяжении следующих месяцев я часто думал об этой
гипотезе, и, честно говоря, почти убедил себя в том, что она неверна. Но
вскоре, к моему удивлению, казалось бы, совершенно не связанные исследования
совместно с Роненом Плессером, который в то время был аспирантом в Гарварде, а
теперь работает в Институте Вейцмана и университете Дьюка, полностью изменили
мое отношение к гипотезе. Плессер и я заинтересовались методами построения
путем математических преобразований новых доселе неизвестных многообразий
Калаби‑Яу из заданного многообразия Калаби‑Яу. Особенно притягательным нам
казался метод орбифолдов, предложенный в середине 1980‑х гг. Диксоном, Джеффри
Харви из Чикагского университета, Вафой и Виттеном. Грубо говоря, этот метод
состоит в склеивании различных точек на исходном многообразии Калаби‑Яу
согласно математической схеме, гарантирующей, что при склеивании снова
получится многообразие Калаби‑Яу. Эта процедура иллюстрируется на рис. 10.4.
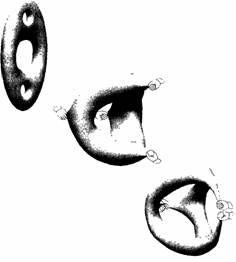 Рис. 10.4. Метод орбифолдов есть процедура построения
нового многообразия Калаби‑Яу путем склеивания различных точек на исходном
многообразии. Рис. 10.4. Метод орбифолдов есть процедура построения
нового многообразия Калаби‑Яу путем склеивания различных точек на исходном
многообразии.
Математические выкладки, стоящие за подобными манипуляциями,
невообразимо сложны, и в этом причина того, что занимающимся струнами
теоретикам удалось детально исследовать эту процедуру лишь применительно к
простейшим многообразиям — многомерным обобщениям торов, изображенных на рис.
9.1. Однако мы с Плессером поняли, что ряд очень красивых утверждений Дорона
Гепнера, работавшего тогда в Принстонском университете, может привести к мощной
теоретической схеме, в рамках которой можно применить технику орбифолдов к
сложным многообразиям Калаби‑Яу, например, к изображенному на рис. 8.9.
После нескольких месяцев напряженной работы в этом
направлении мы пришли к неожиданному выводу. Если склеивать определенные группы
точек правильным образом, получающееся многообразие Калаби‑Яу будет отличаться
от исходного, но совершенно удивительным образом. Число отверстий нечетной
размерности нового многообразия будет равно числу отверстий четной размерности
исходного, и наоборот. Это, в частности, означает, что полное число отверстий,
а, следовательно, и число семейств частиц в двух многообразиях будут
одинаковыми, хотя из‑за четно‑нечетных замен вид многообразий и их
фундаментальные геометрические свойства будут существенно разными.
Воодушевленные очевидной связью с догадкой Диксона‑Лерхе‑Вафы‑Уорнера,
Плессер и я углубились в изучение центрального вопроса: будут ли эти два
различных многообразия с одинаковым числом семейств частиц согласованы по
остальным физическим свойствам? Через пару месяцев кропотливого математического
анализа, подбадриваемые моим бывшим научным руководителем Грэмом Россом из
Оксфорда и Вафой, мы с Плессером пришли к утвердительному ответу. По
математическим соображениям, связанным с четно‑нечетными заменами, мы назвали
эти физически эквивалентные, но геометрически различные пространства Калаби‑Яу
зеркальными многообразиями. Пространства зеркальных пар Калаби‑Яу не являются
в буквальном смысле зеркальными образами друг друга. Но при всем различии
геометрических свойств, если эти пространства используются в качестве
дополнительных измерений теории струн, они приводят к физически эквивалентным
Вселенным.
Недели, последовавшие после того, как результат был получен,
были крайне волнующими. Мы осознавали, что находимся вблизи новой области
физики струн. Мы показали, что изначально установленная Эйнштейном тесная
взаимосвязь между геометрией и физикой в теории струн существенно
модифицируется. Радикально отличающиеся геометрические структуры, которые в
общей теории относительности имели бы различные физические свойства, в теории
струн приводят к эквивалентным физическим моделям. Вдруг мы сделали ошибку?
Вдруг в их физических свойствах имеются тонкие отличия, которые мы не заметили?
Например, когда мы сообщили о своих результатах Яу, он вежливо, но твердо
сказал, что мы, должно быть, ошиблись; по его мнению, с математической точки
зрения наши результаты слишком странные, чтобы оказаться справедливыми. Его
мнение заставило нас взять длительный перерыв для проверок.
Одно дело ошибиться в скромном утверждении, которое мало
кому интересно. Но наш результат был неожиданным шагом в новом направлении, и
неминуемо вызвал бы бурные отклики. Если мы ошибемся, об этом узнают все.
В конце концов, после всех мыслимых проверок и перепроверок,
убежденность в нашей правоте укрепилась, и мы решили опубликовать результат.
Несколькими днями позже, когда я сидел в своем кабинете в Гарварде, зазвонил
телефон. Это был Филипп Канделас из Техасского университета, который сразу же
осведомился, сижу я или стою. Я сказал, что сижу. Канделас сообщил мне, что он
и двое его студентов, Моника Линкер и Рольф Шиммригк, обнаружили
закономерность, услышав о которой, я непременно упаду со стула. Тщательно изучив
огромный набор пространств Калаби‑Яу, моделированных на компьютере, они
обнаружили, что почти все пространства идут парами, отличающимися заменами
чисел четномерных и нечетномерных отверстий. Я ответил ему, что все еще сижу:
мы с Плессером получили тот же результат. Оказалось, что работа Канделаса и
наша работа дополняют друг друга; мы с Плессером пошли на один шаг дальше и
показали, что все физические свойства зеркальных пар одинаковы, а Канделас со
своими учениками показал, что на пары разбивается гораздо большее число
многообразий Калаби‑Яу. Эти две работы и привели к открытию зеркальной
симметрии в теории струн.
|






