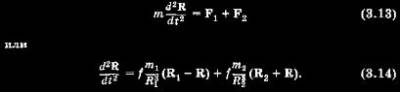3.3. Ограниченная задача трех тел и ее прикладные аспекты
Анализ общей постановки задачи п тел показывает, что учет влияния сил притяжения нескольких планет на движение КА приводит к сложным и громоздким математическим моделям, исследование которых сопряжено со значительными трудностями.
При решении многих задач космической баллистики целесообразно упростить исследование за счет принятия дополнительных допущений. Во-первых, применительно к конкретным задачам межпланетного полета можно выделить небесные тела, оказывающие наибольшее влияние на движение КА, и тем самым ограничить число гравитнрующих тел в общей задаче. В частности, практический интерес представляет случай трех тел (п = 3), получивший название задачи трех тел. Необходимость решения этой задачи была вызвана реализацией в 60-е гг. XX в. лунной программы и полетов Земля—Луна—Земля. В качестве рассматриваемых трех тел принимаются КА, Луна и Земля. Поскольку масса КА намного меньше масс двух других тел, делается допущение о малости притяжения их к КА. Допущение о малости массы одного из тел делает исследование задачи более простым. Эта задача получила специальное название ограниченной задачи трех ТЕЛ; впервые ее сформулировал Л. Эйлер в 1772 г.
Дальнейшие упрощения задачи позволяют получить интересные качественные результаты. Приняты два допущения: притягивающее (гравитирующее) тело с меньшей массой движется относительно тела с большей массой по круговой орбите; движение всех трех тел происходит в одной плоскости. Такую упрощенную задачу называют ограниченной круговой задачей трех тел.
Для удобства исследований считают массу каждого тела сосредоточенной в его центре масс, что позволяет рассматривать (как и раньше) движение материальных точек. При этом материальные точки, соответствующие Луне и Земле, будут двигаться по известным кеплеровым орбитам вокруг общего центра масс.
Перейдем к решению поставленной задачи. Обозначим радиус-вектор негравитирующей материальной точки (КА) относительно общего барицентра (центра масс) через R, расстояния от барицентра до двух гравитирукнцих точек — через R1 и R2 Уравнение движения КА с учетом (3.1) примет вид
Будем рассматривать вращающуюся систему координат, начало которой совмещено с общим центром масс системы трех точек, ось х совпадает с линией, соединяющей точки с массами т1 и т2, ось у лежит в плоскости движения этих точек, а ось z дополняет систему до правой. Обозначим через со угловую скорость обращения точек с массами m1 и т2 относительно оси, перпендикулярной плоскости их движения. В этом случае соотношение (3.14), записанное относительно вращающейся системы координат, примет вид
|