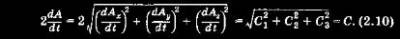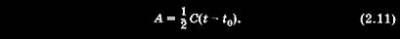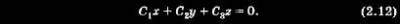Баллистика и навигация космических аппаратов
|
2.2. Интеграл площадей  Нетрудно видеть, что  Здесь dA/dt — секториальная скорость, т. е. приращение площади, описываемой радиусом-вектором движущегося тела за единицу времени. После интегрирования имеем:  Прежде чем сделать некоторые выводы, приведем еще одно важное соотношение. Для его получения умножим интегралы (2.7), (2.8) и (2.9) соответственно на z, x и у и затем сложим полученные результаты:  Соотношение (2.12) — уравнение плоскости, т. е. движение тела под действием центральной силы, приложенной в начале координат (в точке О), происходит в плоскости, проходящей через эту точку. Физически это означает, что силы, не находящиеся в плоскости, содержащей радиус-вектор г движущегося тела и вектор его скорости г, отсутствуют. Положение плоскости (2.12) в пространстве полностью определяют начальными условиями движения. В соответствии с (2.11), (2.12) КА будет двигаться по плоской кривой, сохраняя постоянной свою секториальную скорость и, следовательно, сохраняя постоянными ее проекции на оси координат и величины С1, С2, С3. Если С1, С2, С3 известны, то известны не только величина секториальной скорости, но и ориентация плоскости движения КА. |
Случайные фотографии:
Статьи:
Видео:
Последние новости:
| Варианты внеземной жизни. Часть 1 |
| Солнечная активность |
| Эктазийский период |
| Обнаруженна звезда одна из самых горячих в Галактике |
| HETE-2 оседлал Пегаса |
Видео:
 | Марсианские хроники будущее в настоящем |
| Silicate Crystals Form in Disk of Erupting Star |
| Нибиру и другое... |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2024 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|