Островки стабильности в небесной машине |
 Поведение Солнечной системы совсем не так хорошо описывается уравнениями ньютоновской механики, как думал сам Ньютон. Из-за того, что каждое тело системы взаимодействует со всеми остальными, решить задачу в общем виде невозможно, даже когда в системе всего три тела. Фото (Creative Commons license): Tom Rolfe Меньше месяца осталось путешествовать двум новым космическим обсерваториям — «Гершелю» и «Планку». Месяц прошел и с тех пор, как они покинули французскую ракету «Ариан-5» Европейского космического агентства ESA. Теперь их задача закрепиться в ночном небе в специфической точке, получившей название L2 — второй точке Лагранжа (Lagrangian point). Но вот вопрос: что за сила их там будет удерживать? И почему именно туда и как они там вдвоем поместятся? Попробуем разобраться. Трудности третьего шага классической механики Великому Ньютону (Sir Isaac Newton, 1642–1727) удалось ответить на принципиальный вопрос, мучивший его современников-астрономов. Он показал, что первые астрофизические законы, полученные Иоганном Кеплером (Johannes Kepler, 1571–1630), непосредственно вытекают из открытых им законов движения, если предположить, что между планетами и Солнцем действует сила всемирного притяжения. Более точно: только тогда, когда эта сила обратно пропорциональна квадрату расстояния между Солнцем и планетой, орбита планеты будет замкнутой и эллиптической. Однако, выполняя свой расчет, Ньютон пошел на небольшуюо допустимую подтасовку (заметим в скобках, что умение делать такого рода приближения составляет душу современной науки): он сделал вид, что планеты никак не могут влиять на Солнце. Как бы они ни двигались, Солнце остается на своем месте. А ведь это явно противоречило его же третьему закону: действие равно противодействию. Иначе говоря, каждая планета не только действует на Солнце, но действует с той же самой силой, с какой Солнце действует на планету. Преодолеть это противоречие, сделав второй шаг на пути построения классической механики, оказалось довольно просто. Если речь идет о системе двух тел — например, Земли и Солнца или Земли и Луны, — каковы бы ни были их массы, они будут вращаться вокруг общего центра масс. А все детали этого вращения можно узнать, решив старую ньютоновскую задачу для некого условного тела, массу которого и расстояние от условного неподвижного «солнца» можно легко вычислить по массам реальных тел и расстояниям между ними. Но сделать третий шаг оказалось значительно труднее. Добавление третьего тела решительно портит всю картину. Получить математическое решение в общем виде не удалось и до сих пор. Однако можно достаточно эффективно исследовать различные частные случаи, получая для них приближенные решения. Именно этим и занялись математики времен Великой французской революции Пьер-Симон Лаплас (Pierre-Simon Laplace,1749–1827) и Жозеф Луи Лагранж (Joseph Louis Lagrange,1736–1813). Им-то мы и обязаны возникновением такой науки, как небесная механика — собственно, и название это придумал Лаплас, для которого небесная механика стала обоснованием его философской системы, философии детерминизма.  Жозеф Луи Лагранж. Придуманная им формулировка классической механики получила название Лагранжева формализма и оказалась идеально приспособленной для нужд квантовой теории. Кроме философии, Лапласу мы обязаны эффектными приближенными методами, позволяющими решать важные задачи небесной механики. Например, он придумал, как вычислять движения небесных тел в Солнечной системе, заменяя точечные планеты массивными кольцами: каждая планета полагалась словно бы размазанной по своей орбите. Имя Лагранжа неспециалистам знакомо меньше. Но именно он начал построение аналитической механики (Mécanique analytique), не только ставшей мощным орудием решения практических задач, но и оказавшейся хорошо приспособленной дляквантовой механики. Окружности, стянутые в точки, и точки, размытые в круги Задача трех тел в классической механике значительно упрощается в предположении, что масса первого тела бесконечна по отношению к массе второго, а масса второго — по отношению к массе третьего. В таком предположении нет ничего сумасшедшего: ведь масса Земли в миллиарды раз меньше массы Солнца, а масса даже очень большого искусственного спутника — в миллиарды раз меньше массы Земли. Когда Земля вращается вокруг Солнца, про спутник на орбите можно забыть. Попробуем забыть и про Солнце, рассматривая движение спутника вокруг Земли. Тогда среди множества орбит, по которым спутник может обращаться вокруг Земли, есть одна, лежащая в плоскости земной орбиты, двигаясь по которой, спутник делает полный оборот за год. Что же получается? Спутник делает за год полный оборот вокруг Земли, Земля за этот год совершает полный оборот вокруг Солнца… Не надо обладать редким пространственным воображением, чтобы понять: относительно расположение этих трех тел всегда будет оставаться одним и тем же. Принципиально то, что движения по двум орбитам синхронизированы — в обоих случаях период равен году. Но у спутника есть ещё одна орбита, период движения по которой также равен году. Это та самая орбита, по которой вокруг Солнца движется сама Земля. Оказавшись в любой её точке, спутник не будет изменять своего положения ни относительно Солнца, ни относительно Земли. Но только на этот раз надо забыть уже не о Солнце, а о самой Земле. Одно из самых выдающихся открытий в небесной механике Лагранж совершил в 1772 году, когда решил считать равными нулю не сами отношения массы Земли к массе Солнца и массы спутника к массе Земли, а их квадраты. Он сразу обнаружил, что от целой земной орбиты останется всего три «синхронных» точки, а «годичная» орбита вокруг Земли слегка растянется, и на ней останется только две точки — те, что лежат на прямой, проходящей через Землю и Солнце. Эти пять точек Лагранж называл точками либрации, а мы их теперь называем точками Лагранжа. Оказавшись в одной из них, спутник будет находиться в состоянии равновесия. Точкой L2 называют ту, что располагается в земной тени. Оказавшись в ней, спутник комфортно прикроется от Солнца и не будет улетать далеко от Земли, что обеспечит ему надежную связь с ЦУПом. Главная проблема с L2 заключается в том, что, хотя спутник, очутившись в ней, будет находиться в состоянии равновесия, равновесие это будет неустойчивым: достаточно сколь угодно малого возмущения — хотя бы удара микроскопического метеорита — и спутнику придется для возвращения в L2 включать двигатели. 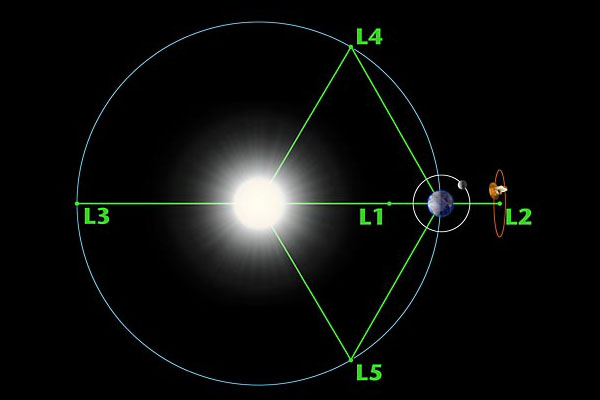 Одно из главных достижений механики Лагранжа — нахождение стационарных решений задачи трех тел, когда все три тела имеют сильно различающиеся массы. В этом случае стационарных решений оказывается пять. То есть, оказавшись в одной из пяти обозначенных точек, спутник, если смотреть на него с Земли, будет неподвижен относительно Солнца. Иллюстрация: WMAP team/NASA Однако переход от идеального к реальному приводит не только к стягиванию окружностей в точки — некоторые точки, напротив, размываются в окружности. И вокруг L2 образуется множество концентрических окружностей, по которым спутник будет двигаться, словно по орбите невидимого небесного тела. Именно на две таких «орбиты» и должны к концу июля выйти «Планк» и «Гершель». Конечно, они не будут там висеть неподвижно по отношению к Земле и Солнцу, Но перемещения их будут столь невелики, что они никогда не выйдут из земной тени, и свет Солнца не помешает им смотреть в ночное небо. Где-то там их уже поджидает космический телескоп WMAP (Wilkinson Microwave Anisotropy Probe), исследующий реликтовое излучение. А со временем туда же прибудет и спешащий на смену «Хабблу» телескоп «Уэбб». Слово фантастов В силу своих особенностей точки Лагранжа привлекают внимание писателей-фантастов. Точка L1 находится между Землей и Солнцем. В книге Артура Кларка (Sir Arthur Charles Clarke, 1917–2008) и Стивена Бакстера (Stephen Baxter) «Солнечная буря» (Sunstorm) именно в ней космические строители возводят огромный экран, призванный загородить Землю от сверхмощной солнечной бури. Пока этого нет, зато там уже трудятся космические аппараты NASA SOHO (Solar and Heliospheric Observatory) и WIND. Ещё две точки Лагранжа — L4 и L5 — находятся на орбите Земли, одна впереди, а другая — позади нее. Главное же отличие двух этих точек Лагранжа от остальных состоит в том, что равновесие оказавшихся в них небесных тел будет устойчивым. На этом и основывается популярная среди астрономов гипотеза, что в окрестностях точек L4 и L5 могут находиться остатки газопылевого облака эпохи формирования планет Солнечной системы, завершившегося 4,5 миллиарда лет назад. Поискать остатки газопылевого облака — но на этот раз того, из которого сформировался наш единственный естественный спутник — можно и в точках L4 и L5 в системе Земля–Луна. И тогда могут выясниться интересные обстоятельства из прошлого нашей планеты. К точкам L4 и L5 к сентябрю 2009 года должны долететь зонды-близнецы STEREO-A и STEREO-B, так же как и SOHO, ориентированные на исследования Солнца. Сравнительно недавно первоначальные планы проекта STEREO были существенно расширены, и в настоящее время на зонды возложена также и задача исследовать окрестности точек Лагранжа на предмет наличия там астероидов. Авторство этой идеи принадлежит Ричарду Харрисону (Richard Harrison) из Лаборатории им. Резерфорда и Апплетона (Rutherford Appleton Laboratory) в британском Оксфордшире. Тем самым астрономы рассчитывают проверить компьютерные модели, предсказывающие наличие астероидов в «устойчивых» точках Лагранжа.  Спутники STEREO должны будут обследовать одну из самых загадочных областей вблизи орбиты Земли. Возможно, точки Лагранжа L4 и L5 системы Солнце–Земля до сих пор удерживают вблизи себя остатки одной из исчезнувших планет Солнечной системы. Иллюстрация: STEREO/NASA В связи с этим следует сказать, что во второй половине ХХ столетия, когда появилась возможность численно решать на компьютере сложные уравнения небесной механики, образ стабильной и предсказуемой Солнечной системы — а вместе с ним философия детерминизма — окончательно ушли в прошлое. Оказалось, что неизбежная неточность в численных значениях скоростей и координат планет в данный момент времени приводит к весьма существенным различиям в сценариях эволюции Солнечной системы. Так, в одном из сценариев Солнечная система через сотни миллионов лет может даже лишиться одной из своих планет… Судьба Теи Компьютерные модели дают уникальную возможность реконструировать события, происходившие в удаленной от нас эпохе молодости Солнечной системы. Широкую известность получила модель сотрудников Принстонского университета (Princeton University) математика Эдварда Бельбруно (Edward Belbruno) и астрофизика Ричарда Готта (Richard Gott). Согласно этой модели, в полном соответствии с законами небесной механики, в одной из точек Лагранжа (L4 или L5) сформировалась в далеком прошлом планета Тея (Teia). Из-за гравитационного воздействия со стороны остальных планет Тея в некоторый момент времени покинула точку Лагранжа, вышла на траекторию движения к Земле и в конечном итоге столкнулась с ней. Модель Готта и Бельбруно детализирует гипотезу, которой придерживаются многие астрономы и согласно которой Луна состоит из вещества, образовавшегося после соударения с Землей космического объекта размером с Марс около четырех миллиардов лет назад. Проблемным местом этой гипотезы всегда был вопрос о том, где именно такой объект мог образоваться. Если бы Земля столкнулась с объектом, прилетевшим из внешней части Солнечной системы, то его энергия была бы очень большой, и результатом соударения с Землей стало бы не создание Луны, а разрушение Земли. Следовательно, образоваться подобный объект должен был бы где-то недалеко от Земли — и окрестности одной из точек Лагранжа были бы вполне подходящим местом. Но если подобное развитие событий могло иметь место в прошлом, что запрещает им произойти в будущем? Иными словами, не вырастет ли в окрестности L4 или L5 ещё одна Тея? Этот вопрос озаботил корреспондента журнала New Scientist. Но: «Это невозможно», — успокоил его профессор Пол Вейгерт (Paul Weigert) из канадского университета в Западном Онтарио (University of Western Ontario). По его словам, в настоящее время в Солнечной системе недостаточно пылевых частиц для формирования таких объектов — это четыре миллиарда лет назад, в эпоху образования планет из частиц газопылевых облаков, ситуация была принципиально иной. «Сейчас слишком мало вещества для того, чтобы смогло сформироваться что-нибудь столь же значительное по размерам», — говорит Вейгерт. В то же время в окрестностях точек Лагранжа вполне могут находиться астероиды — остатки «строительного материала» планеты Теи. Такого мнения придерживается, например, упомянутый выше Ричард Готт. Он уверен, что для Земли такие астероиды могут стать заметным фактором риска. Действительно, гравитационное воздействие со стороны других планет (в первую очередь Венеры) может оказаться достаточным для того, чтобы астероид покинул окрестность точки Лагранжа, а в этом случае он вполне может выйти на траекторию столкновения с Землей. Как считает Готт, «если мы действительно обнаружим в окрестности точки Лагранжа большой астероид, самым правильным было бы вытащить его оттуда и разбить его на отдельные фрагменты»  Кинофильм «Троя». Лагерь троянцев. Обнаруженные вблизи точек L4 и L5 системы Солнце–Юпитер скопления астероидов получили название лагерь ахейцев и лагерь троянцев — в полном соответствии с традицией переносить на небо античную историю. Фото: Warner Bros. Гипотеза Готта о находящихся в точках Лагранжа астероидах появилась не на пустом месте. Ещё в 1906 году они были обнаружены в точках Лагранжа системы Солнце–Юпитер. Это открытие сделал немецкий астроном Макс Вольф (Maximilian Franz Joseph Cornelius Wolf, 1863–1932), и это были первые астероиды за пределами пояса астероидов между Марсом и Юпитером. Впоследствии в точках Лагранжа системы Солнце-Юпитер их было обнаружено более тысячи. Однако поиски астероидов вблизи других планет Солнечной системы были не столь успешными. По-видимому, их все же нет около Сатурна, и только лишь в последнем десятилетии они были обнаружены недалеко от Нептуна. Вполне понятно, что вопрос о наличии астероидов в точках Лагранжа системы Земля–Солнце чрезвычайно волнует современных астрономов. Да, впрочем, и не только их. Пол Вейгерт, используя телескоп на Мауна-Кеа на Гавайях, уже пытался отыскать их в начале 90-х годов. Его наблюдения были весьма напряженными, однако успеха не принесли. Сравнительно недавно стартовали программы автоматического поиска астероидов — в частности, Линкольновский проект поиска близких к Земле астероидов (Lincoln Near-Earth Asteroid Research project). Пока и они не принесли результата. Сейчас главная надежда обнаружить опасность, грозящую Земле из точек L4 и L5, возлагается на зонды STEREO. Поначалу даже обсуждалась возможность навсегда оставить их в окрестности этих точек. Расчеты, однако, показали, что остановка зондов там потребовала бы слишком большого расхода топлива, и пришлось остановиться на варианте медленного пролета данных областей пространства. Приборами, с помощью которых будет осуществляться программа поиска, должны стать размещенные на борту зондов гелиосферные регистраторы. Но даже в этом случае задача остается весьма сложной. На будущих снимках астероиды будут всего лишь точками, перемещающимися на фоне тысяч звезд. Предполагается, что активную помощь в поисках окажут астрономы-любители, которые будут просматривать полученные снимки в Интернете. Главная интрига предстоящих наблюдений связана с тем, что никто не знает, сколько астероидов должны «увидеть» зонды СТЕРЕО (если увидят вообще). Анализ новых компьютерных моделей, разработанных командой Пола Вейгерта, сделал ситуацию ещё менее предсказуемой: оказалось, что гравитационное воздействие Венеры может не только «вытаскивать» астероиды из точек Лагранжа, но и запускать обратный процесс, способствуя их перемещению в эти точки. Сам Вейгерт полагает, что общее количество астероидов в окрестности точек Лагранжа не очень велико («в любом случае речь не идет о сотнях») и что по размеру они на два порядка меньше тех, которые образуют пояс астероидов между Марсом и Юпитером. Подтвердятся ли его прогнозы? Ждать осталось совсем немного… Борис Булюбаш
|
Статьи:
Видео:
Последние новости:
| Туманность Гума — остаток сверхновой звезды |
| Солнечный свет на кольцах Сатурна |
| Космические брокеры играют на повышение |
| Пожар на Земле |
| Мантия Земли |
Видео:
 | Einstein's Cosmic Speed Limit |
 | BBC. Космос (часть 2) |
 | Webb Model Construction Timelapse |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


