Волны чего?
Явление интерференции, открытое Дэвиссоном и Джермером,
реально продемонстрировало, что электроны подобны волнам. Но при этом возникает
естественный вопрос: волнам чего? Одно из первых предположений на эту тему,
сделанное австрийским физиком Эрвином Шредингером, заключалось в том, что эти
волны представляют собой «размазанные» электроны. Это предположение отчасти
улавливало «сущность» электронной волны, но было слишком неточным. Когда вы
размазываете что‑нибудь, часть его находится здесь, а другая часть в другом
месте. Однако никому и никогда не приходилось иметь дело с половиной или с
третью, или с иной частью электрона. Это усложняло понимание того, что
представляет собой размазанный электрон. В 1926 г. немецкий физик Макс Борн
существенно уточнил предложенную Шредингером интерпретацию электронной волны, и
именно этой интерпретацией, усиленной Бором и его коллегами, мы пользуемся и
сегодня. Утверждение Борна касается одного из самых странных свойств квантовой
теории, тем не менее, оно подтверждается огромным количеством экспериментальных
данных. Согласно этому утверждению электронная волна должна интерпретироваться
с точки зрения вероятности. В тех областях, где амплитуда (или, точнее, квадрат
амплитуды) волны больше, обнаружение электрона более вероятно; в местах, где
амплитуда мала, вероятность обнаружить электрон меньше. Пример показан на рис.
4.9.
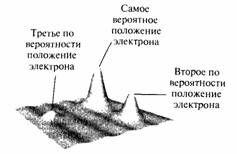 Рис. 4.9. Волна, ассоциированная с электроном, имеет
наибольшую амплитуду в тех местах, где обнаружение электрона наиболее вероятно;
амплитуда волны убывает по мере уменьшения вероятности обнаружения электрона.
Это действительно необычная идея. Какое отношение имеет
вероятность к формулировке фундаментальных законов физики? Мы привыкли к тому,
что вероятность присуща лошадиным бегам, подбрасыванию монеты или игре в
рулетку, но в этих случаях она просто является отражением неполноты нашего
знания. Если мы точно знаем скорость колеса рулетки, вес и твердость шарика,
который бегает по нему, положение и скорость шарика в тот момент, когда он
падает на колесо, свойства материала ячеек и т. п., и если мы используем для
наших вычислений достаточно мощные компьютеры, мы можем, в соответствии с
законами классической физики, совершенно точно предсказать, где остановится
шарик. В казино полагаются на неспособность игрока получить всю эту информацию
и провести необходимые вычисления перед тем, как сделать ставку. Однако ясно,
что вероятность, с которой приходится сталкиваться во время игры в рулетку, не
отражает никаких фундаментальных свойств Вселенной. Напротив, квантовая
механика вводит понятие вероятности в устройство мироздания на гораздо более
глубоком уровне. Согласно утверждению Борна, подкрепленному собранными более
чем за полвека экспериментальными данными, наличие у материи волновых свойств
подразумевает, что фундаментальное описание материи должно иметь вероятностный
характер. Закон де Бройля показывает, что для макроскопических объектов, таких
как кофейная чашка или рулеточное колесо, волновые свойства являются
практически ненаблюдаемыми, и в обычных ситуациях связанная с ними квантово‑механическая
вероятность может полностью игнорироваться. Но этот же закон говорит, что на
микроскопическом уровне мы, в лучшем случае, можем указать только вероятность
того, что электрон будет обнаружен в любом заданном месте.
Допустим, что электронные волны обладают теми же свойствами,
что и все другие волны, например, они могут сталкиваться с препятствиями и
образовывать вторичные волны. Однако в рамках вероятностного описания из этого
не следует, что сам электрон распадается на части. Это означает лишь, что
имеются области, в которых электрон может появиться с ненулевой вероятностью.
На практике это означает, что если мы будем снова и снова повторять совершенно
одинаковым образом какой‑либо эксперимент с электроном, касающийся, например,
измерения его положения, мы не будем всегда получать одинаковый результат.
Повторяющиеся эксперименты дадут набор различных результатов, в которых частота
появления электрона в заданном месте будет функцией плотности вероятности
электронной волны. Если функция плотности вероятности для волны (или, точнее,
квадрат плотности вероятности) для точки А в два раза больше, чем для точки В,
то при многократном повторении опыта мы увидим, что электрон будет
обнаруживаться в точке А в два раза чаще, чем в точке В. Точный результат
эксперимента не может быть предсказан; лучшее, что можно сделать — предсказать
вероятность данного возможного исхода.
Однако если математическое выражение для функции плотности
вероятности известно точно, то даже при такой неопределенности исходов
вероятностный прогноз может быть проверен путем многократного повторения эксперимента,
что позволяет экспериментально определить вероятность того или иного
конкретного результата. Всего через несколько месяцев после появления гипотезы
де Бройля Шредингер сделал важный шаг в этом направлении, предложив уравнение,
которое определяет форму и эволюцию таких вероятностных волн, или, как они
теперь называются, волновых функций. Вскоре уравнение Шредингера и
вероятностная интерпретация были использованы для получения фантастически
точных предсказаний. Таким образом, к 1927 г. классическая наивность была
утрачена. Ушли те дни, когда Вселенная представлялась работавшим как часы
механизмом, объекты которого, приведенные в движение в какой‑то момент в
прошлом, покорно следовали к неизбежному, единственным образом определяемому
пункту назначения. Согласно квантовой механике Вселенная развивается в
соответствии со строгими и точными математическими законами, но эти законы
определяют только вероятность того, что может наступить то или иное конкретное
будущее, и ничего не говорят о том, какое будущее наступит в действительности.
Многие сочтут этот вывод обескураживающим или даже
совершенно неприемлемым. Одним из таких людей был Эйнштейн. В одном из наиболее
известных в истории физики высказываний он предостерегал сторонников квантовой
механики: «Бог не играет в кости со Вселенной». Он считал, что вероятность
появляется в фундаментальной физике по той же причине, по которой она
появляется в игре в рулетку: вследствие существенной неполноты нашего знания. С
точки зрения Эйнштейна, во Вселенной нет места для будущего, точное содержание
которого включает элементы вероятности. Физики должны предсказывать, как будет
развиваться Вселенная, а не определять вероятность того, что события могут
пойти каким‑то путем. Но эксперимент за экспериментом (некоторые из наиболее
впечатляющих были выполнены уже после его смерти) убедительно подтверждали, что
Эйнштейн был не прав. Как заметил однажды по этому поводу британский физик‑теоретик
Стивен Хокинг. «Заблуждался Эйнштейн, а не квантовая теория».
Тем не менее, споры о том, что же в действительности
представляет собой квантовая механика, не утихают. Все согласны в том, как
использовать уравнения квантовой механики для получения точных предсказаний.
Нет согласия в вопросах о том, что в действительности представляют собой
волновые функции, каким образом частица «выбирает», какому из многих вариантов
будущего ей следовать. Нет согласия даже в вопросе о том, действительно ли она
выбирает или вместо этого разделяется, подобно разветвляющемуся руслу реки, и
живет во всех возможных будущих, в вечно расширяющемся мире параллельных
вселенных. Эти интерпретации сами по себе заслуживают отдельной книги, и, в
действительности, есть немало превосходных книг, пропагандирующих тот или иной
взгляд на квантовую теорию. Но совершенно определенным кажется тот факт, что
независимо от интерпретации квантовой механики, она неопровержимо доказывает,
что Вселенная основана на принципах, которые являются неестественными с точки
зрения повседневного опыта.
Общий урок, который дают теория относительности и квантовая
механика, состоит в том, что в ходе глубоких исследований основ мироздания
можно столкнуться с фактами, которые очень сильно отличаются от наших ожиданий.
Отвага при постановке новых вопросов может потребовать непредвиденной гибкости,
когда нам придется принимать неожиданные точки зрения.
|
