Расчет орбиты кометы
Если удалось провести наблюдения трех положений кометы, можно выполнить первый расчет ее траектории, причем лучше всего, если моменты этих трех наблюдений значительно различаются. Однако это требование вступает в противоречие с необходимостью определить орбиту кометы как можно в более короткий срок. Определение первого положения кометы (когда она только что обнаружена) производится при помощи зарисовок, не обеспечивающих, естественно, высокой точности, в результате чего первые расчеты орбиты почти наверняка будут далекими от реальности. При быстром движении кометы расчет ее орбиты облегчается, поскольку здесь меньше сказываются ошибки отдельных измерений наблюдаемых положений кометы.По своей форме орбита кометы весьма вытянута, что отличает ее, например, от орбиты планеты. Поэтому в первом пробном расчете можно принять, что орбита кометы параболическая. Еще Кеплер установил, что орбиты небесных тел, вращающихся вокруг Солнца, представляют собой кривые второго порядка, а Солнце находится в одном из фокусов этих кривых. Кривые второго порядка получаются при пересечении конуса плоскостью в различных направлениях (рис. 20).Так, линия пересечения поверхности конуса плоскостью, параллельной его основанию, представляет собой окружность. При разрезе конуса плоскостью, слегка наклоненной к основанию, получается эллипс. При увеличении наклона получаем кривые пересечения более сложного характера. Когда секущая плоскость параллельна одной из образующих конуса, в сечении получается, парабола, а при еще большем наклоне секущей плоскости к основанию — гипербола. Рис. 20. Образование кривых второго порядка при пересечении конуса плоскостями: 1 — окружность; 2 — эллипс; 3 — парабола; 4 — гипербола
Обозначим через а величину большой полуоси эллипса, а через q — расстояние от точки эллипса, ближайшей к точке фокуса F, до самого фокуса. Отношение разности между а и q к величине а носит название эксцентриситета (рис. 21): е=(а—q)/а. Эксцентриситет окружности равен нулю, эксцентриситет же вытянутого эллипса может быть весьма велик. Эксцентриситет параболы равен единице, а эксцентриситет гиперболы больше единицы.Определение орбиты небесного тела состоит в нахождении шести числовых величин — элементов орбиты. Три из них показывают, а каком направлении в космическом пространстве движется небесное тело. Еще две величины определяют форму и размеры орбиты, и, наконец, последняя указывает, в какой точке своей орбиты находится тело в данный момент. Форма орбиты определяется ее эксцентриситетом е. Если известно, что орбита параболическая, то е = 1, и одной из неизвестных величин становится меньше.Представление о размерах орбиты дает величина а. В случае параболической орбиты а является бесконечно большой величиной, и тогда размеры орбиты можно охарактеризовать перигелийным расстоянием ц, В случае эллиптической орбиты его можно определить по формуле q = а( 1—е). Единицей для измерения а и q служит астрономическая единица расстояний, равная среднему расстоянию между Землей и Солнцем. Рис. 21. Схема, поясняющая определение эксцентриситета эллипса
Орбита любого небесного тела, вращающегося вокруг Солнца, целиком расположена в одной плоскости, носящей Название плоскости орбиты (рис. 22), причем Солнце обязательно располагается в этой плоскости. Плоскость орбиты Земли совпадает с плоскостью эклиптики и пересекается с плоскостями орбит других небесных тел под некоторыми углами. Угол между плоскостью орбиты небесного тела и плоскостью эклиптики носит название угла наклонения орбиты i.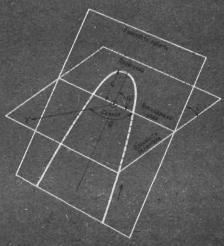 Рис. 22. Элементы орбиты (стрелкой указано движение небесного тела по орбите)
Точка, в которой небесное тело пересекает плоскость эклиптики при движении из Южной полусферы неба в Северную, носит название восходящего узла. Точка же, в которой небесное тело пересекает эту плоскость при движении из Северной полусферы неба в Южную, называется нисходящим узлом. Угол между направлением на точку весеннего равноденствия и направлением на восходящий или нисходящий узел называемся долготой узла орбиты небесного тела. При атом долгота восходящего узла обозначается знаком n, а долгота" нисходящего узла — обозначается u.
Положение плоскости орбиты небесного тела в пространстве определяется двумя величинами — i и n. На то, как эта орбита ориентирована в своей плоскости, указывается величиной ш — углом между направлениями на восходящий узел и на точку перигелия.
Таким образом определяются все особенности орбиты в целом. Чтобы рассчитать, в какой точке орбиты должно находиться небесное тело в некоторый момент времени, используется величина t0 — время, прошедшее с момента прохождения небесным телом точки перигелия. Зная tо, можно на основании законов Кеплера рассчитать положение тела на орбите в любой момент времени.
Кроме того, в качестве вспомогательных величин применяются среднее суточное движение п, период обращения Р и долгота точки перигелия — все они легко вычисляются с помощью только что рассмотренных шести элементов орбиты.При наблюдении небесного тела можно определить его эклиптические координаты, но нельзя непосредственно измерить расстояние тела от Солнца или от Земли. Определение орбиты небесного тела, в сущности, сводится к определению расстояний до него в разные моменты времени. Прежде всего производят расчет положений Земли в пространстве на моменты трех проведенных наблюдений. Затем, задав некоторую величину расстояний между кометой и Землей на момент второго наблюдения, с помощью законов Кеплера вычисляют расстояния между Землей и кометой на моменты первого и третьего наблюдений. Наконец, произведя расчет эклиптических координат кометы на моменты первого и третьего наблюдений, сравнивают полученные данные с результатами действительных наблюдений.
Если обозначить величины, полученные в результате наблюдений, через О («обсерватус»), а величины, полученные в результате расчетов, через С («компутатус»), то, вероятно, разница О—С не будет равна ,нулю. Если повторить указанные расчеты, слегка изменив задаваемую величину расстояния, то, очевидно, вновь полученная величина разности О—С будет отличаться от предыдущей. При дальнейшем изменении величины предполагаемого расстояния можно добиться, чтобы величина разности О—С стала близка к нулю. Подобный метод постепенного приближения к истинной величине искомого параметра носит название метода последовательных приближений и довольно широко применяется в астрономии.
Когда величина разности О—С станет Незначительно отличаться от нуля, можно считать, что орбита кометы вполне определена. Теперь необходимо произвести расчет будущих положений кометы, что позволило бы планировать дальнейшие ее наблюдения. Обычно при этом выясняется, что величина разности расчетных и фактически наблюдаемых положений кометы (то есть О—С) со временем возрастает. В таком случае, используя результаты новых наблюдений, вносят поправку в расчеты орбиты. Поскольку на этот раз результаты наблюдений охватывают более длительный период, то очевидно, имеется возможность более точно рассчитать орбиту кометы.
Чтобы при определении орбиты кометы быстро выяснить, насколько нужно изменить первоначально заданную предположительную величину расстояния в следующем приближении, требуются необходимый опыт и сноровка. Опытные и искусные в этом деле люди, если они имеют дело с не очень сложным случаем расчета орбиты, могут достичь цели, так сказать, с четвертого захода. Для неискушенных людей даже весьма многочисленные новые приближения могут и не позволить получить оптимальную величину разности О—С, Безусловно, что применение современных ЭВМ позволяет получать необходимый результат без особых затруднений.
Часто, предположив орбиту кометы параболической, вы обнаруживаете, что величина разности О—C С начинает увеличиваться со временем при продолжительном периоде наблюдений. В этом случае необходимо произвести тщательный перерасчет орбиты. С этой целью надо внимательно проверить результаты наблюдений положений кометы, исключив возможность больших ошибок. Кроме того, желательно внести необходимые поправки, учитывающие, что наблюдения производились с поверхности Земли, то есть привести результаты к такому виду, как если бы наблюдения производились из центра Земли. Нелишне также учесть возможное влияние на движение кометы со стороны притяжения Земли и крупных планет. Возможно, что в результате проделанной работы вы придете к выводу, что имеете дело либо с сильно удлиненной эллиптической орбитой с эксцентриситетом, близким к единице, либо с гиперболической орбитой, эксцентриситет которой больше единицы.
|
