Царство Солнца
|
Глава 6. Что удерживает миры на месте Почему Луна не падает? Дело было в 1666 г., когда Исааку Ньютону было двадцать три года. Он учился в Кембридже, но в районе Лондона началась ужасная чума, так что Ньютон жил в доме матери, в сельской местности. Сидя на крыльце и задумчиво глядя в сад, он увидел, как с ветки дерева сорвалось яблоко и полетело на землю. В этом не было ничего странного. Всем было известно, что предметы падают на землю. Аристотель даже утверждал, что это свойственно земным вещам: они стараются оказаться как можно ближе к центру Земли. Но тогда взгляд Ньютона скользнул к небесам, где сиял бледный полумесяц, почти терявшийся в свете солнца. Почему же Луна не надает? Аристотель ответил бы на это утверждением, что Луна не земная, поэтому исходно не имеет тенденции падать. Или же он мог бы сказать (и Птолемей или даже Коперник с ним согласились бы), что Луна закреплена на небесной сфере и не может упасть, даже если бы у нее была такая тенденция. Однако прошло уже больше пятидесяти лет с тех пор, как Кеплер доказал, что никаких небесных сфер не существует. Тогда что же удерживает Луну наверху? Ньютон не первым задумался над этим. Галилей и Кеплер оба размышляли над тем, какие силы могут удерживать планеты на их орбитах. Ведь планеты вращались вокруг Солнца, а второй закон Кеплера показывал, что планета двигается тем быстрее, чем ближе она к Солнцу. Действительно, казалось, что планеты должна удерживать какая-то сила, принадлежащая самому Солнцу, которая становится тем сильнее, чем ближе они подходят к нему. Кеплер считал, что в Солнце сконцентрировала какая-то магнетическая сила, которая и удерживает планеты на их орбитах. Поскольку эта сила иногда является притяжением, а иногда — отталкиванием, то орбита искажается до эллипса за счет толчков в противоположные стороны. Это объяснение было не слишком убедительным, но, по крайней мере, Кеплер был на нужном пути. И вот теперь Ньютон попытался создать такую систему, которая была бы совершенно убедительной. Если человек быстро вращает ведро с водой у себя над головой, вращение создает силу, которая давит на воду в направлении, противоположном центру вращения. Вода прижимается к дну ведра и не выливается даже в тот момент, когда ведро переворачивается вверх дном, оказываясь у вас над головой. Сила, действующая от центра, называется центробежной. Вращаясь вокруг Земли, Луна создает центробежную силу, которая отталкивает ее от Земли. Эта сила будет противодействовать силе притяжения Земли (той самой, которая действовала на яблоко). Совместно эти силы могут уравновешиваться, и Луна останется на своей орбите навечно. Во-первых, какова сила притяжения Земли па расстоянии до Луны? (Поскольку именно сила земного притяжения дает предметам вес, то ее называют гравитацией, от латинского слова «вес».) Ньютон мог получить размер силы притяжения на поверхности Земли, зная скорость, с которой предметы — такие, как яблоки, — надают на землю. Эта сила может исходить из центра Земли, поскольку, похоже, именно гуда и направляется яблоко. (Если вы выкопаете яму, то яблоко упадет на ее дно и будет падать настолько глубоко, насколько вы пожелаете углубиться.) Но что, если вы поднимете яблоко высоко в воздух, так что оно окажется намного дальше от центра Земли, чем когда находилось у ее поверхности? Если сила притяжения будет по-прежнему действовать на яблоко, то, видимо, потому, что эта сила распространяется наружу от центра Зб^ли, как надуваемый воздушный шарик. Но поверхность увеличивающегося, воздушного шарика увеличивается по мере totq, как шар становится больше. Более того, поверхность увеличивается как квадрат диаметра. Если диаметр шара удвоен, то площадь увеличится в 2 х 2, или в 4 раза. Если бы диаметр увеличился в 5 раз, то площадь увеличилась бы в 5 х 5, или в 25 раз. 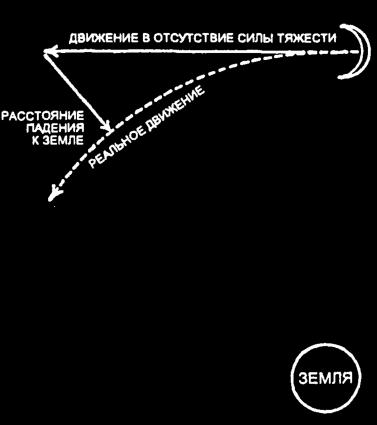 Падающая Луна Но поверхность увеличивающегося, воздушного шарика увеличивается по мере totq, как шар становится больше. Более того, поверхность увеличивается как квадрат диаметра. Если диаметр шара удвоен, то площадь увеличится в 2 х 2, или в 4 раза. Если бы диаметр увеличился в 5 раз, то площадь увеличилась бы в 5 х 5, или в 25 раз. Если бы сила тяжести распространялась над поверхностью Земли, как воздушный шар, то она распространялась бы на поверхность, которая возрастала бы как квадрат расстояния от центра Земли. При этом сила бы рассредоточивалась и становилась все более слабой. На поверхности Земли предмет находился на определенном расстоянии от центра и сила тяжести имела определенную величину. Если бы этот предмет был поднят в космос до тех пор, пока он не окажется вдвое дальше от центра Земли, чем когда он находился на поверхности, то сила тяжести распределится по 2 * 2 раза большей поверхности и станет в 2 * 2, или в 4 раза слабее. Или, если вы предпочитаете, она будет в 1/4 раза сильнее, чем на поверхности. Если бы предмет был поднят на расстояние, в 10 раз превышающее расстояние от центра Земли до ее поверхности, то сила тяжести уменьшилась бы до 1/00 первоначальной силы. Для расстояний до центра Земли и от центра Земли до Луны Ньютон использовал самые точные цифры, которые были на тот момент доступны. И теперь он смог рассчитать, какой будет сила земного притяжения вблизи Луны. Затем он вычислил, насколько быстро Луна должна была бы двигаться на орбите, чтобы уравновесить силу притяжения Земли. Однако его цифры показали, что Луне пришлось бы двигаться быстрее, чем она двигалась на самом деле. В чем была ошибка? Ньютон усомнился в том, что он был прав, предположив, что Земля притягивает предметы только к своему центру. В конце концов, различные части Земли могли притягивать Луну в чуть разных направлениях. Ньютон не знал, как именно можно было бы учесть такую возможность, и потому отказался от этой мысли. |
Статьи:
Видео:
Последние новости:
| Голубые бродяги в NGC 6397 |
| Стивен Хокинг скоро отправится в космос |
| Огннные шары (рассказывают следователи) |
| Весовой ценз для примадонн |
| Лазерная связь с инопланетянами |
Видео:
 | Mini Soccer Balls in Space |
 | Медицина на орбите |
 | НЛО - Факты и Мистификации 2-5 |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2024 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


