Баллистика и навигация космических аппаратов
|
14.5. Скользящий спуск Тяжелый перегрузочный режим (пятах > 8) в сочетании с большим разбросом точек приземления делает непригодными аппараты баллистического типа для регулярных полетов с человеком на борту. Только на первом этапе развития космической техники, когда относительная простота реализации играет решающую роль, оправдано применение СА баллистического типа. Для уменьшения максимальных перегрузок необходимо увеличивать время движения СА в плотных слоях атмосферы (см. (14.9)), осуществляя снижение по более пологим траекториям по сравнению с баллистическим спуском. Эта задача может быть решена путем использования СА, обладающих аэродинамической лодъемной силон (см. (14.1)). Даже небольшое значение аэродинамического качества приводит к существенному уменьшению максимальных перегрузок. При разработке аппаратов, обладающих подъемными силами, проводили поиски форм, располагающих максимальным значением коэффициента лобового сопротивления, на которых можно получить подъемную аэродинамическую силу — качество СА. Отмеченные обстоятельства способствовали появлению аппаратов так называемого скользящего спуска, базирующихся на формах для СА баллистического типа и отличающихся большими значениями коэффициентов лобового сопротивления (Сх > 1) и подъемной силы (С > 03...0,5) при небольшом значении качества (К ~ 0,2...0,4). Достигают это следующим образом. Рассмотрим рис. 14.10, на котором схематически изображен аппарат сегментно-кониче-ской формы, представляющий собой тело вращения с сегментной лобовой поверхностью СА и конической задней поверхностью. При симметричном обтекании подобной формы (при а = 0) подъемная сила будет отсутствовать, т. е. спуск будет баллистическим. В случае несимметричного обтекания (а * 0) появляется вертикальная составляющая аэродинамической силы — подъемная сила {К - О). Режим спуска СА такой формы с а * 0 можно обеспечить приложением реактивных управляющих сил, создающих необходимую величину угла атаки а на траектории снижения — управление с помощью изменения угла атаки. Но существует и другой путь. Сместим центр масс СА вверх от оси симметрии. 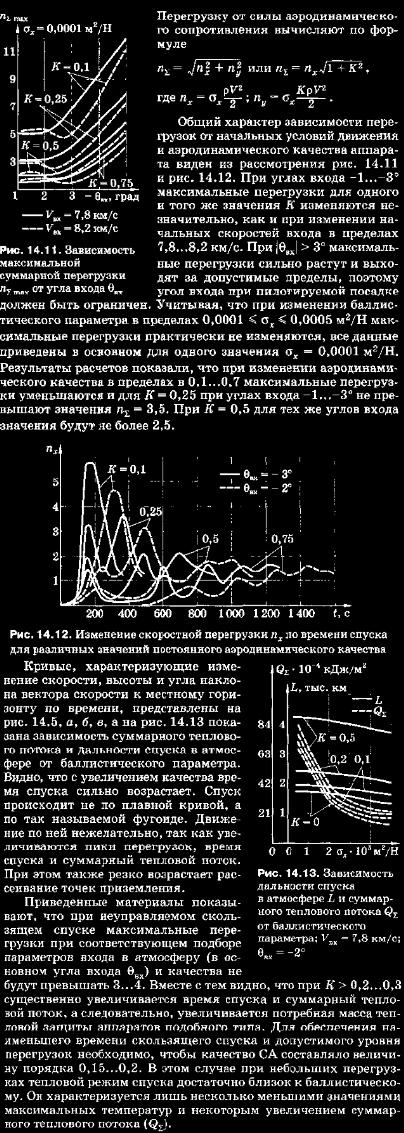 Тогда спуск такого аппарата будет проходить под некоторым балансировочным углом атаки а = о^ * 0, так как появляется момент относительно центра масс от силы лобового сопротивления, который будет уравновешиваться моментом от подъемной силы (см. рис. 14.10). При этом реактивное управление для обеспечения режима спуска а = а6 = const необходимо только для парирования разного рода возмущений. Необходимо отметить важный момент: вектор подъемной силы всегда лежит в одной плоскости (плоскости симметрии аппарата), про ходящей через центр масс и центр давления. В силу этого, разворачивая аппарат на угол у относительно оси, соединяющей центр масс с центром давления, или скоростной оси (назовем у углом крена), мы будем изменять проекцию подъемной силы на вертикальную плоскость симметрии СА. Значение подъемной силы при полете на балансировочном угле атаки а = сц и при угле крена у = 0 обозначим через Уб. Тогда вертикальная составляющая ГЕ при у ** 0 равна Ув = Уб cos у и соответственно горизон-тальйая Уг = Уб sin у. Таким обраъом, появляется возможность не только получить подъемную силу У6, но и изменять ее в полете от YB = Уб до Ув = -Уб посредством изменения угла крена. В силу того, что СА практически статически нейтрален при вращении относительно оси «ц. м. — ц. д.», управляющий момент, потребный для разворота и удержания аппарата на некотором угле у, очень незначителен, при этом его величину определяют d основном возможной величиной момента сопротивления, возникающего из-за технологической несимметричности аппарата, неравномерного уноса массы при обгаре тепловой защиты и т. д. В этом заключается очень большое достоинство СА, управляемых с помощью изменения угла крена. Необходимо отметить, что спуск аппаратов скользящего типа на основном участке траектории (при числах М > 4.. .5) протекает практически с постоянным углом атаки с^. Поэтому достаточно обосновано допущение о постоянстве коэффициентов лобового сопротивления Сх, подъемной силы Су и соответственен но аэродинамического качества Кб = ^ (а = а6). Аппараты скользящего типа удобно характеризовать баллистическим параметром ot и располагаемым значением качества А"расп> за которое принимается значение качества Кб при полете с углом атаки а = о,:Д;расп = Яе. Вертикальная составляющая аэродинамического качества, называемая ЭФФЕКТИВНОЙ, как и подъемная сила, зависит от угла крена у: К^ = #б cos у. В соответствии с этим говорят об управлении с помощью изменения угла крена или об управлении «эффективным качеством». Из изложенного выше ясно, что приземление аппаратов скользящего типа должно производиться теми же средствами, что и аппаратов баллистического типа, ибо малое располагаемое аэродинамическое качество не позволяет осуществить планирующую посадку. В заключение необходимо отметить, что наряду с возможностью управления формы СА с сегментной лобовой поверхностью имеют и ряд других существенных достоинств по сравнению, например, с СА шаровых форм: ► удобство компоновки, связанное в первую очередь с размещением экипажа и оборудования; ► относительно небольшие скорости СА к моменту ввода в поток парашютной системы приземления. Действительно, за счет большого значения Сх скорость движения СА к моменту ввода не превышает 100...200 м/с; ► реализация на СА аэродинамической подъемной силы возможна без применения специальных устройств; ► масса потребной тепловой защиты СА сегментной формы меньше массы потребной тепловой защиты СА шаровой формы на = 20% (при равных условиях). Это объясняется тем, что находящиеся за лобовым сегментом в «аэродинамической тени» части аппаратов подвергаются меньшему тепловому воздействию и соответственно их меньше надо защищать от теплового воздействия. Неуправляемый спуск СА скользящего типа с постоянным значением аэродинамического качества требует лишь простейшей стабилизации аппарата по крену. Рассмотрим прежде всего перегрузки и время их действия на траекториях указанного типа.  УПРАВЛЕНИЕ АППАРАТАМИ СКОЛЬЗЯЩЕГО ТИПА. Использование аппаратов скользящего типа без управления аэродинамической подъемной силой нецелесообразно в первую очередь из-за значительного разброса точек приземления, существенно превышающего рассеивание при баллистическом спуске. Вместе с тем наличие подъемной силы позволяет осуществлять управление спуском с целью выполнения различных задач. Управление аппаратами скользящего типа наиболее целесообразно осуществлять с помощью изменения угла крена. Этот путь отличается достаточной простотой и минимальными потребными затратами рабочего тела на стабилизацию СА. Программное изменение в процессе снижения угла крена (изменение вертикальной состав ляющей подъемной силы) позволяет осуществить спуск по траекториям, удовлетворяющим поставленным условиям. Процесс изменения в полете угла крена СА с целью выведения аппарата в заданную точку фазового пространства или выдерживания определенной оптимальной траектории осуществляется системой управления спуском (СУС). При решении различных задач к СУС могут предъявляться самые широкие требования в зависимости от целевого назначения объекта. В одних случаях основным условием может быть построение СУС минимальной массы, обеспечивающей приемлемую точность посадки, а в других — требование исключительно точной посадки т. д. Путей построения СУС в настоящее время достаточно много. Каждой системе присущи свои преимущества и недостатки в отношении обеспечиваемой точности посадки, надежности, массовых затрат, потребных бортовых и наземных средств, простоты реализации и т. д. В силу этого приходится отдавать предпочтение той или иной системе в каждом конкретном случае в зависимости от поставленных задач и имеющихся средств. * Первым этапом построения СУС является определение номинальной программы изменения управляющего параметра (номинальное управление), обеспечивающей снижение СА по определенной заданной (программной) или вырабатываемой в процессе полета траектории. В общем случае поставленные условия могут выполняться при движении по самым различным траекториям. Задача номинального управления состоит в том, чтобы определить это семейство траекторий и обеспечить движение СА по ним в номинальных условиях, т. е. при отсутствии возмущений. * Второй этап построения СУС состоит в определении закона изменения управляющего параметра, обеспечивающего спуск аппарата по выбранной номинальной траектории (или, по крайней мере, по траектории, близкой к номинальной) в реальных условиях — при действии разного рода возмущений. Одной из основных особенностей построения СУС аппаратов скользящего типа является необходимость управления продольной и боковой дальностью полета с помощью одного управляющего параметра — угла крена. В этом случае управление боковой дальностью может быть организовано только в рамках управления продольной дальностью полета путем переворотов СА «с боку на бок» в определенные моменты на траектории спуска. Аппарат будет двигаться по колеблющейся кривой относительно заданного направления движения. В моменты переворота система управления фактически размыкается и может быть нарушено условие устойчивости управления продольной дальностью. Отмеченный фактор существенно затрудняет построение СУС для СА скользящего типа. Другой особенностью, которую необходимо принимать во внимание при построении СУС, является то, что на аппаратах скользящего типа управляющую силу на участке основного аэродинамического торможения нельзя убрать (обнулить), ибо СА движется в атмосфере с постоянным углом атаки а = ctg * О и соответственно Су6 ф О. Третья особенность состоит в следующем. Ввиду того, что величина располагаемого аэродинамического качества у аппаратов скользящего типа мала (К6 - 0,2...0,4), возможности управления определяются в основном общим запасом энергии СА и, следовательно, убывают по мере снижения, т. е. по мере гашения скорости аппарата. В настоящее время одним из основных требований к спуску аппаратов скользящего типа является обеспечение их посадки в заданном районе ограниченных размеров. Возможности обеспечения точной посадки характеризуют зоной или областью маневра, которую определяют пол ура зн остью максимальной и минимальной дальностей полета (в продольном и боковом направлениях), достигаемых на данном СЛ. В том случае, когда величина предполагаемого рассеивания за счет действия разного рода возмущающих факторов существенно меньше возможной зоны маневра (т. е. имеется избыток в величине управляющей силы — качества аппарата), можно говорить о построении оптимальной по некоторому критерию траектории спуска. Рассмотрим построение оптимальной с точки зрения минимума потребной массы тепловой защиты СА (GT-S) траектории снижения. Наиболее естественно в этом случае принять «прямой» критерий Gt э = min. (14.12) Однако из-за больших математических трудностей решить задачу в такой постановке не удается. Обычно применяют какой-либо косвенный критерий, определенным образом связанный с массой тепловой защиты. Проведенные исследования позволили сделать очень важный вывод: для аппаратов с сублимирующей теплозащитой условие (14.12) выполняется на траекториях с минимальным временем атмосферного участка спуска (£сп = min). Решение задачи в такой постановке существенно упрощается. Найдем выражение для времени спуска в плотных слоях атмосферы tcn — tK - tBX, которое будем минимизировать. Проведя те же рассуждения, что и при выводе соотношения (14.8) (см. (14.3)), получим 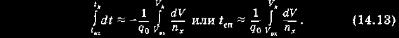 Решение задачи проведем с учетом ограничения на максимально допустимую перегрузку nmax« лдоп. (14.14) В такой постановке очевидно, что минимум функционала tcn = rain будет достигаться на траектории, в каждой точке которой перегрузка пх (а следовательно, и суммарная перегрузка, так как Къ — const) максимальна. Однако обеспечить спуск аппаратов по изоперегрузочной траектории от момента входа в плотные слои атмосферы (Ла, Квх) и до момента раскрытия парашютной системы (Ак, VK) невозможно из-за малого значения плотности на высотах, близких к Авх, и малых скоростей спуска на высотах, близких к Лк. Оптимальная траектория будет состоять из трех участков: движение по ограничению (участок И) и вне ограничения (участки I, III на рис. 14.14). Для решения поставленной задачи надо дополнительно минимизировать время f, и tK на участках движения вне ограничения, т. е. на участке выхода и схода с ограничения. Решение задачи минимизации времени от входа в плотные слои атмосферы до выхода на ограничение (14.14) показало, что оптимальным управлением является программа одноразового «переключения» аэродинамического качества с ~К6 на +Й"б. Точку переключения определяют с учетом начальных условий входа и величины допустимой максимальной перегрузки. После достижения максимума перегрузок необходимо мгновенно уменьшить эффективное значение качества для удержания СА на ограничении (14.14). В дальнейшем происходит увеличение 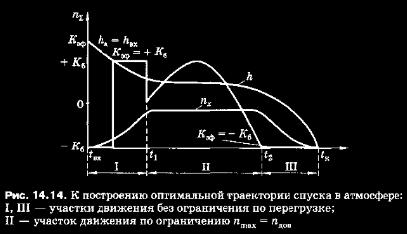 эффективного качества для предотвращения сваливания в зону недопустимых перегрузок, а затем, по мере гашения скорости полета — уменьшение для предотвращения ухода с ограничения. И хотя в дальнейшем аппарат выходит на минимальное значение качества К^ — -Кб, перегрузки начинают уменьшаться. Минимум времени спуска на участке III обеспечивается при спуске с АГ^ф = Полное время спуска уменьшается по мере увеличения допустимой перегрузки, и в пределе при снятии ограничения (14.14) минимум времени обеспечивается на траекториях спуска с К3ф = -К6. Необходимо отметить, что при построении оптимального управления совершенно не говорилось о требовании точной посадки в заданном районе Земли. Во многих случаях введение этого и некоторых других конкретных условий существенно видоизменяет оптимальное управление. Во-первых, орбиты спутников могут быть такими, что не всегда можно получить оптимальные условия входа, удовлетворяющие требованию посадки в заданном районе Земли. Во-вторых, СА должен располагать определенными маневренными возможностями, чтобы парировать возмущения и обеспечить точную посадку. В силу отмеченных и ряда других обстоятельств при практической реализации не удается добиться абсолютно оптимального решения, а приходится несколько отступать от него с целью выполнения всех условий. Первоочередное требование точной посадки в заданном районе Земли способствовало тому, что в настоящее время наибольшее распространение получили простейшие номинальные траектории с постоянным значением эффективного аэродинамического качества (или угла крена). В зависимости от реальных начальных условий входа в атмосферу может быть установлено такое значение угла крена (эффективного качества), которое обеспечивает приход СА в заданный район (естественно, в пределах зоны маневрирования). Номинальные траектории, определяемые движением на постоянном значении аэродинамического качества, приводят к более тяжелому тепловому режиму СА по сравнению с рассмотренными выше оптимальными траекториями. Но отход от оптимальности тем меньше, чем меньше располагаемое качество СА, и при Ярасп < 0,3 во многих случаях использование неоптимальных номинальных траекторий практически оказывается более целесообразным (учитывая, в первую очередь, простоту реализации). Еще раз отметим, что при спуске с орбиты ИСЗ значение качества « 0,1...0,15 является достаточным для существенного облегчения перегрузочного режима (максимальные значения перегрузок не превышают 4...5). Небольших запасов эффективного качества в пределах 0,10. ..0,15 относительно номинального значения в целом достаточно для парирования действующих на СА возмущений. Потребное номинальное значение эффективного качества определяют условиями входа аппарата в плотные слои атмосферы и заданной точкой посадки. В заключение следует отметить следующее: применение угла крена у в качестве единственного управляющего параметра вызывает необходимость распорядиться последним так, чтобы обеспечить одновременно продольное и боковое управление. Общее решение этой задачи состоит в раздельном использовании модуля и знака угла у в одном из двух вариантов: ► изменение модуля подчиняется требованиям продольного управления, изменение знака у — требованиям бокового; ► обратное распределение модуля и знака у. При этом управление с помощью изменений знака у по смыслу является дискретным, благодаря чему в конце траектории появляется неуправляемый участок, на котором образуется некоторый конечный промах по соответствующей координате. Первый вариант более удобный, универсальный, точный, так как в этом случае для решения наиболее сложной части задачи (формирования и стабилизации траектории в продольной плоскости) применяют более совершенное управление (модулем угла у), а более грубое управление (знаком угла у) — для решения задачи ликвидации относительно небольших боковых отклонений. ПРОСТЫЕ СИСТЕМЫ УПРАВЛЕНИЯ НЕПРЕРЫВНОГО ДЕЙСТВИЯ. Требование точной посадки С А в заданном районе Земли является в настоящее время доминирующим, и система управления спуском должна обеспечить его выполнение при соблюдении некоторых ограничений, в первую очередь по перегрузкам. Это определило целое направление в построении СУС — управление конечной дальностью полета. Сделаем два принципиальных замечания. ^ Правильнее было бы говорить об управлении конечным состоянием объекта, так как конечные условия включают не только дальность полета, но и скорость и траекторный угол на заданной конечной высоте. Однако, как показали проведенные исследования, тормозных свойств аппаратов скользящего типа достаточно, чтобы обеспечить необходимые начальные условия для работы, например, парашютно-реактивной системы мягкой посадки независимо от величины реализуемой дальности полета. Это и позволяет при построении СУС контролировать только дальность полета (в общем случае — продольную и боковую). ф При построении СУС для аппаратов скользящего типа обычно не учитывают движение СА на заключительном участке (участок работы СМП), т. е. конечную точку принимают на высоте начала работы СМП. Это приводит к дополнительному рассеиванию точек посадки на поверхности Земли. Например, при действии ветра со средней скоростью ~ 10 м/с за время спуска на парашюте СА может отнести на величину = 10 км относительно точки посадки, определяемой без учета заключительного участка. Различают следующие принципы синтеза сус непрерывного действия: ► с использованием заранее рассчитанных программных зависимостей; ► с прогнозированием точки посадки; ► смешанного типа, когда по результатам прогноза выбирают программную зависимость. Наиболее простыми являются СУС первого типа. Простые СУС — это системы, которые строят с использованием простой, легко доступной для измерений информации; обработку этой информации (для выдачи управляющего сигнала) производят на простейших вычислителях или простых аналоговых устройствах. В настоящее время можно считать, что такой простой информацией является измерение перегрузок, интегралов от перегрузок и времени полета. При этом наиболее простую СУС получают, если перегрузки измеряют в осях, жестко связанных с корпусом СА. При проектировании СУС непрерывного действия необходимо определить некоторую функцию фазовых координат (функционал управления), поддержание значений которой близкими к расчетным позволяет получить необходимую точность приземления. В качестве такой функции можно рассматривать отклонение точки приземления от заданной ДLK = LK - 1Н0М, которое должно быть равно нулю. Здесь LK — конечная дальность полета, т. е. дальность, отсчитываемая по поверхности Земли от точки входа в плотные слои атмосферы (или от момента включения ТДУ) до точки посадки; £яом — требуемая конечная дальность полета. Считая, что действующие на СА возмущения невелики, отклонение точки посадки (в продольной плоскости движения) можно записать  является желательным для простейших СУС, ибо ее получение сопряжено с достаточными трудностями. В целом методическая ошибка информации в связанной системе координат должна быть оценена в каждом конкретном случае и сопоставлена с требованиями точности посадки. Отметим только, что одной из принципиальных (и очень существенной) ошибок, определяющих точность этой информации, является ошибка в балансировочном угле атаки. Причина ее возникновения заключается в следующем: измеритель перегрузок выставляется под каким-то определенным (в пределе нулевым) углом к предполагаемой скоростной оси СА. Но при реальном снижении балансировочный угол атаки из-за разного рода неучтенных факторов может отличаться от расчетного. В этом случае будет иметь место ошибка в получаемой ия борту скорости и соответственно в дальности полета. Величина этого отклонения пропорциональна отношению проекций суммарной перегрузки на направление акселерометра и на направление действительного вектора скорости. Отметим, что определенной оптимальной установкой оси акселерометра фор1 эту составляющую ошибки можно несколько уменьшить. Например, считая отклонение балансировочного угла До^ и ошибку в качестве СА ДК (сц) зависимыми величинами с нормальным законом распределения и дисперсией о2а и оптимальный угол выставки акселерометра может быть найден из выражения  применение подобных СУС требует обеспечения достаточно точной установки чувствительных элементов и малых уходов ги-роплатформы в процессе снижения. Отметим, что функционал (14.17) принципиально может быть реализован с использованием и одного интегрирующего акселерометра с переменным направлением оси чувствительности [12]. # Третий вариант — простые СУС непрерывного действия. Из приведенных выше данных следует, что для реализации функционала типа (14.15) необходимо, помимо интегрирования перегрузок, дифференцировать их, а также иметь гиростабилизи-рованную платформу с двумя интегрирующими акселерометрами или одним акселерометром с переменным направлением, т. е. эти системы можно определить как *не очень простые». Во многих случаях применяют простые системы, работающие с минимальной информацией при самой простой ее обработке. К таким системам относят прежде всего СУС, использующие информацию с одного интегрирующего акселерометра. Ось этого акселерометра или жестко связана с корпусом СА (псв), или установлена определенным образом в инерциальном пространстве (пин). На борту СА запоминается программная зависимость изменения перегрузок псв или лня в функции используемого в СУС аргумента. Чаще всего в качестве аргумента берут кажущуюся скорость Т/8св или Vs ин. По величине рассогласований перегрузок Дгасв = (ясв)1ек - (псв)пр или Дгаин = (яин)тек - (пин)пр на программной и текущей траектории формируют управляющий сигнал Ay = \ An. Коэффициент может быть постоянным во все время спуска или переменным по траектории. Это определяют требованиями, предъявляемыми к точности посадки СА. Отметим также, что на борту СА может запоминаться несколько программных зависимостей псв или пин. В реальном полете в функции от имеющихся начальных условий входа СА в плотные слои атмосферы выбирают ту или иную программу, обеспечивающую наилучшее выполнение поставленных условий. В некоторых случаях вместо рассогласований перегрузок используют рассогласования по времени спуска на текущей и программной траекториях. Управление боковым движением в описанных системах осуществляют путем переворотов СА «с боку на бок» в некоторых определенным образом выбранных точках траектории. Причем для простых СУС точки переворота, как правило, фиксированы. Подобные простые СУС имеют существенные методические ошибки. Так, при спуске с орбиты ИСЗ они обеспечивают посадку с разбросом в пределах нескольких десятков км по дальности и в боковом направлении. Это и определяет возможную область их применения. СИСТЕМЫ ДИСКРЕТНОГО УПРАВЛЕНИЯ ДАЛЬНОСТЬЮ ПОЛЕТА КА. Построение алгоритма для системы дискретного управления может быть проведено с использованием метода попадающих траекторий [12, 62]. Траектории, полет корабля по которым приводит к попаданию в заданную точку, т. е. обеспечивается достижение заданной дальности, при обязательном выполнении ограничений по перегрузкам пплх < лдоп называют попадающими. Метод попадающих траекторий при управлении дальностью полета возвращающегося космического корабля целесообразно применять по следующим причинам. При решении задачи попадания в заданную точку фазового пространства нет необходимости компенсировать влияние возмущений в каждой точке траектории, выбранной на основании обработки измерений на самом начальном участке спуска в атмосфере. Имеется целое семейство траекторий, движение по которым позволяет выполнить поставленные условия. Поэтому рационально рассматривать задачу парирования не текущих отклонений параметров движения от поминальных, а конечного отклонения регулируемого параметра. В нашем случае — это обеспечение минимума рассеивания точек посадки при выполнении поставленных ограничений по перегрузкам и аэродинамическому нагреву. Требование же вести полет по одной траектории должно приводить к чрезмерной нагрузке на СУС, нерациональному расходу рабочего тела. Следует указать и второе важное соображение в пользу применения дискретных систем. Оно следует из того, что снижающийся в атмосфере аппарат обладает огромной энергией. Поэтому, если на какой-то момент времени t, на СА подействовало возмущение (или управление), то только спустя некоторое время At траектория заметно отойдет от невозмущенной. Одним словом, реально существует какое-то время At, зависящее от величины действующих возмущений, необходимое для выяснения текущей картины спуска и принятия уверенного решения по управлению. При этом чем проще состав бортовых средств и ниже их чувствительность и быстродействие, тем больше величина At. Рассмотрим один из возможных путей управления при дискретном корректировании траектории в ее характерных точках с использованием семейства попадающих траекторий. При синтезе системы управления по этому пути исходят из того, что на траектории спуска существует т точек, в которых можно изменять величину управляющей силы таким образом, что возмущения будут парированы. Места проведения коррекций можно фиксировать или выбирать на борту аппарата в зависимости от действующих возмущений или от величины отклонения текущей траектории от расчетной и т. д. Принцип действия автономной системы управления, строящийся с использованием предлагаемого метода, следующий. В момент достижения аппаратом фиксированного значения аргумента системы р - р0 по полученной на борту информации определяют некоторый постоянный угол крена у0 (в общем случае — программу), с которым осуществляют дальнейший полет. В момент достижения аргументом значения р = р1 по результатам сравнения величины некоторого функционала, вычисленного по данным бортовых измерений, с некоторым предвычислен-ным значением проводят коррекцию первоначального угла Yj == Yo + В последующие моменты pt = р2, р3.....рт проводяткоррекции аналогичным способом соответственно значениям yif у2, ..., ут. Причем коррекции проводят таким образом, чтобы на каждом этапе осуществлялся перевод на ближайшую попадающую траекторию. Таким образом, выбором угла у0 (в момент р = р0) определяется расчетная траектория первого приближения. При действии разного рода возмущений параметры действительной траектории будут отличаться от параметров расчетной траектории. Поэтому в последующие моменты полета на основании продолжающихся бортовых измерений проводят корректировки текущих значений качества 1, 2, ..., т-го приближений в некоторых характерных точках траектории (при заданных фиксированных значениях аргумента). Резюмируя, отметим, что согласно методу попадающих траекторий, построение системы осуществляют в предположении, что на каждом этапе полета (от коррекции до коррекции) корабль летит по ближайшей попадающей траектории из всей их возможной совокупности. Проведенные исследования показали, что построение СУС в самом простом варианте реализации метода попадающих траекторий позволяет обеспечить точность посадки порядка 20...30 км; этот метод можно эффективно использовать для спуска автоматических капсул. АЛГОРИТМЫ УПРАВЛЕНИЯ, РЕАЛИЗУЕМЫЕ С ПОМОЩЬЮ БОРТОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ. Существующие в настоящее время бортовые цифровые вычислительные машины (БЦВМ) позволяют реализовать алгоритмы управления с прогнозом движения наперед [62]. В этом случае структура управления очень гибка и позволяет в процессе полета получить значительный объем информации о движении и на основании ее перестраивать алгоритмы управления. Очевидно также, что с по мощью БЦВМ можно реализовать самые различные алгоритмы, обеспечивающие решение поставленной задачи. При синтезе СУС с БЦВМ следует различать три основных участка снижения СА: ► активный, где работает тормозная двигательная установка (ТДУ); за счет тяги на аппарат действуют перегрузки; ► движение в разреженных слоях атмосферы (до высоты Ла = = 100 км), где перегрузки практически отсутствуют; ► движение в плотных слоях атмосферы, где действуют перегрузки за счет аэродинамических сил. Точную посадку СА обеспечивают путем управления аэродинамической силой на третьем участке траектории при соответственно выбранной точке включения ТДУ. К моменту начала этого участка компоненты вектора состояния, рассчитанные БЦВМ, будут отличаться от действительных главным образом за счет ошибок в заданиц начальных данных. Для выявления этих погрешностей необходимо использовать дополнительную информацию о траектории. Наличие БЦВМ открывает новые возможности в навигации КА на участке спуска. Применительно к задаче безопасного спуска аппарата с БЦВМ в заданную точку поверхности навигация предполагает решение следующих основных задач на борту СА: ► определение вектора состояния СА в фазовом пространстве и всей необходимой информации о характеристиках корабля и окружающей среды (задача навигации СА); ► определение с необходимой дискретностью требуемых значений управляющего параметра для выполнения условий полета (задача наведения СА). Для определения на борту компонентов вектора состояния СА используют обычное дифференциальное уравнение   Здесь п,, V: (j = 1, 2, 3) — соответственно проекции векторов суммарной перегрузки и скорости на оси инерциальной системы координат. ф Вне зависимости от стратегии выбора управления можно утверждать, что к моменту окончания участка управляемого полета шаг коррекции At следует уменьшать, чтобы свести к минимуму элементы случайности в обеспечиваемой точности. Это соображение подсказывает, что в начале спуска At можно задавать побольше, а к концу — поменьше. Это, в свою очередь, позволяет наилучшим образом построить процесс вычисления управляющего воздействия и снизить требования к ВЦВМ, ибо из двух алгоритмов управления, использование которых в СУС с БЦВМ обеспечивает одинаковую точность, предпочтение всегда будет отдано тому алгоритму, реализация которого предъявляет менее жесткие требования к БЦВМ. Наиболее целесообразным путем в этом направлении является использование переменного шага коррекций и числа итераций (здесь итерация — один просчет на БЦВМ траектории спуска «вперед»). В начале спуска шаг коррекции по возможности следует брать наибольшим (Ai„), а для вычисления управления — использовать специальные приближенно-аналитические зависимости или проводить одну-две итерации. Предположим, что мы используем для расчета управления одну итерацию. Зная полное время спуска ten, с помощью системы уравнений для расчета прогнозируемой траектории определим требования к БЦВМ в ля виси мости от первоначального шага коррекции Д tn. Очевидно, что эти требования будут тем жестче, чем меньше AtH. В рамках сформулированной задачи максимизировать At„ удается с помощью следующего простого приема. После того как СА пролетел по времени половину пути, т.е. до конца остается —, можно или удвоить число итераций, или вдвое сократить шаг коррекции ~2~ • По истечении еще четверти пути по временидо конца остается j можно: а) использовать для расчетовчетыре итерации, или б) в четыре раза уменьшить шаг коррекции , или в) а два раза уменьшить шаг коррекции и проводить две итерации. Чем ближе к окончанию участка спуска, тем число возможных вариантов улучшения качества управления возрастает. В целом этот путь дает хорошие результаты, ф Для парирования бокового отклонения точки посадки от расчетной целесообразно применять следующий метод (рис. 14.15). Расчет траектории «вперед» в ускоренном масштабе времени осуществляют со значением угла крена, знак которого противоположен знаку действительного значения. Здесь используют практическую независимость продольной дальности полета до точки посадки от знака угла крена (ДL < 1 км). При этом определяют величину бокового отклонения точки посадки при предполагаемой смене знака угла крена в момент следующей коррекции. После того как значение прогнозируемого бокового отклонения точки посадки попадает в некоторую допустимую окрестность относительно расчетной точки, определяемой требуемой точностью посадки, следует действительный переворот СА «с 5оку на бок» — смена знака угла крена. Можно ограничиться двумя такими переворотами на траектории. При использовании в СУС алгоритмов управления, основанных на рассмотренном подходе, может быть обеспечена точность посадки в пределах З...5км в продольном и боковом направлениях при действии возможных возмущений с учетом динамики движения по крену и существующих приборных ошибок. |
Статьи:
Видео:
Последние новости:
| Как иначе обнаружить внеземные цивилизации |
| Марсианский сфинкс |
| Юпитер, Ио и его тень |
| Варианты внеземной жизни. Часть 2 |
| Лучшие 30 снимков АМС «Кассини» |
Видео:
 | SOFIA Flight Tests for Early Science Progress |
 | Луна: иная реальность (4 из 5) |
 | НЛО вторжение на землю (1/6) |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2024 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


