Баллистика и навигация космических аппаратов
|
13.6. Синтез стратегий сближения на основе теории нечеткого управления Отметим, что идеология методов управления сближением КА за многие годы развития космонавтики не претерпела серьезных изменений. Техническая реализуемость их как в автоматическом, так и телеоператорном режимах была многократно апробирована и доказала свою жизнеспособность и эффективность. Однако, что касается телеоператорного режима, осуществляемого на этапе причаливания (стыковки), то, ссылаясь на интервью летчика-космонавта СССР, руководителя полетом ОК «Мир» и МКС В. А. Соловьева, можно утверждать, что «...и сегодня это нестандартная операция: с близкого расстояния она получается, а с дальнего — нет». Ситуация с реализацией этого режима настолько исключительна, что будет уместным воспроизвести здесь фрагмент указанного интервью, касающийся истории имевшего место соударения грузового корабля «Прогресс» с модулем «Спектр» ОК «Мир». Опуская очень интересные, но не имеющие прямого отношения к обсуждаемому научно-техническому вопросу комментарии, ограничимся изложением существа: «Корабль, будучи в неуправляемом режиме, врезался в станцию на скорости 3 м/с и нарушил герметичность модуля. Благодаря достаточно решительным действиям экипажа удалось спасти жизнь станции в целом, но неприятностей натерпелись мы предостаточно. У нас до этого много чего было: и пожары, и короткие замыкания, но та — самая серьезная нештатная ситуация*. Подобный режим был до этого реализован дважды (речь идет о выполнении стыковок В. Джанибековым и В. Соловьевым с Л. Кизимом. — Коммент. авт.) Но! Тогда экипаж летал, находясь внутри транспортного корабля, а здесь предполагалось стыковаться как бы виртуально: экипаж внутри станции и в помощь ему телекамера, установленная на корабле «Прогресс» (имея в виду приведенную в предшествующем параграфе классификацию, данный вариант наведения соответствует схеме наведение «на себя». —Коммент. авт.). Первый раз, двумя-тремя месяцами раньше, у этого же экипажа стыковка не получилась: «просвистели» недалеко от станции. Особых выводов, увы, мы не сделали. И решили, как того требовала техническая ситуация, повторить операцию. При всех сближениях с орбитальной станцией у нас используются так называемые пролетные, безопасные траектории: активный корабль при своем движении при наведении на пассивную станцию-матку все время промахивается: это касается и кораблей «Прогресс», и «Союзов». Задача экипажа этот промах непрерывно уменьшать, в конце концов достигая желаемого результата — стыковки. И если в какой-то момент экипаж просто не понимает, что происходит, куда он летит, достаточно отпустить ручку управления и реализуется схема пролетной траектории (причем время для этого есть: счет идет на минуты). Циблиев (речь идет о командире экипажа летчике-космонавте Василии Циблиеве. — Коммент. авт.) этого не сделал. Конечно, для принятия подобного решения нужна моральная смелость: невыполненное задание никогда никого не радовало) К сожалению, все происходило вне зоны видимости с Земли: помочь она ничем не могла». Описанная ситуация представляет собой идеальный пример, позволяющий проиллюстрировать [65] возможности применения теории нечеткого управления, показать путь к более надежному, а в перспективе квазиоптимальному по энергетическим затратам способу решения задач, требующих при задействовании оператора-космонавта в контуре управления сближением различной точности выполнения процессов стыковки, инспекционного пролета и др. С помощью этой теории могут быть синтезированы существенно нелинейные законы на основе адекватных по сложности моделей движения, гарантирующие достижение приемлемого качества управления в широком диапазоне варьирования параметров объекта и возмущающих воздействий, диапазон изменений которых задается так называемыми «нечеткими множествами». Предметом теории нечеткого управления является изучение методов синтеза стратегий (законов) управления на основе нечетких правил управления, выраженных в словесном виде: «если некоторое отклонение А велико, то управление U должно быть большой отрицательной величиной» и т. п. Эти правила управления (лингвистические высказывания по управлению) формулируют обычно на основе накопленного опыта оператора ручного управления. Для лучшего понимания сути теории нечеткого управления рассмотрим элементарный гипотетический пример ручной стыковки КА, по содержанию близкий обсуждаемому случаю. Предположим, что в процессе сближения активный КА (АКА) движется по траектории, соответствующей номинальной по оценкам осуществляющего управление космонавта. Последний командует себе: «так держать». Если траектория АКА ниже или выше требуемой, то оператором будет отработана «внутренняя» команда «немного выше» или «немного ниже». Причем в зависимости от величины оцененного «на глазок» отклонения эта команда может быть в определенном смысле конкретизирована, например, «резко и много выше (или ниже)». Подобный алгоритм прост и понятен, однако здесь необходимо сделать несколько замечаний. Во-первых, оценивание космонавтом «на глазок» возникших отклонений не может претендовать на высокую точность, тем более при неоднократно зафиксированных в реальных полетах случаев неадекватного восприятия и оценки пространства, времени или собственных движений (см., например: Г. Т. Береговой и др. Моделирование систем полуавтоматического управления космических кораблей / Под ред. А. И. Яковлева. — М.: Машиностроение, 1986. — С. 10). Во-вторых, понятия «сильно», «слабо», «немного» и т. д. являются, строго говоря, субъективно неопределенными, и возможность эффективной отработки соответствующих словесных нечетких правил в значительной степени будет определяться интуицией и опытом оператора (космонавта в нашем примере). На изучение процесса «синтеза» закона управления при этом может уйти от нескольких часов до нескольких дней, а «доводка» контура управления потребует нескольких недель работы на тренажере и на натурном объекте. Но, вместе с тем, полученный таким образом «контур управления» может обладать достаточно высоким качеством в широком диапазоне изменения внешних условий и динамических параметров объекта. Из сказанного вытекают также отрицательные стороны эмпиризма: неточность сформулированных высказываний, трудность экстраполяции имеющегося опыта на новые условия применения, и особенно на новые, еще не существующие образцы техники. Очевидно, что человеческий разум всегда будет превосходить искусственный интеллект. Тем не менее стремление к развитию методологии синтеза законов управления по схеме: от словесных нечетких правил управления к четким, точным и гибким действиям с помощью модели и натурного объекта — представляется конструктивным. Именно этим обстоятельством объясняется наличие большого количества публикаций, посвященных проблемам применения теории нечеткого управления при создании ряяличных систем. ОБОБЩЕННАЯ ПОСТАНОВКА ЗАДАЧИ И ПОДХОД К ЕЕ РЕШЕНИЮ. Рассмотрим управляемое движение объекта, описываемое системой нестационарных нелинейных дифференциальных уравнений общего вида  Может показаться, что объем требуемых вычислений чрезмерно велик. Однако необходимо подчеркнуть, что начальное приближение оказывает здесь большую роль на ход всех последующих шагов. В нашем случае здравое мышление квалифицированного специалиста с помощью теории нечеткого управления приобретает вид вполне четкого закона управления, и этот закон используют в качестве первого приближения, что позволяет существенно сократить число перебираемых вариантов. Естественно, в пределах настоящего материала невозможно изложить результаты исследований, касающихся применения «нечеткого» подхода ко всему многообразию задач сближения КА. В связи с этим отметим, что настоящий анализ возможности синтеза стратегий сближения ограничивается обсуждением вопросов управления на участке сближения, непосредственно предшествующего процессу стыковки. В качестве возможных «канонических» вариантов методов сближения рассматривают методы маневрирования активного КА в окрестности пассивной станции, подробно описанные в [52]. МЕТОДЫ УПРАВЛЕНИЯ СБЛИЖЕНИЕМ, ИСПОЛЬЗУЮЩИЕ ИНФОРМАЦИЮ О ПОЛОЖЕНИИ ЛИНИИ ВИЗИРОВАНИЯ. Методы данной группы относят к методам наведения, не использующим полную информацию о траекториях сближающихся КА. Рассмотрим метод прямого наведения (метод погони) в визирной системе координат. Модель движения вдоль линии визирования для него задают дифференциальным уравнением вида [23]: 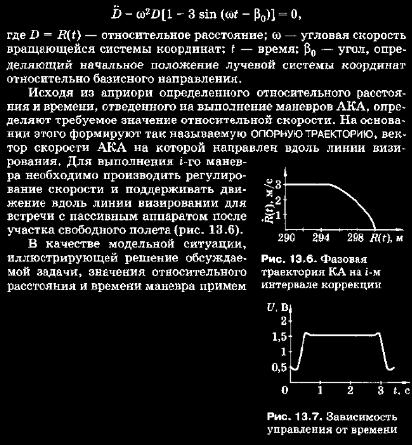 равными соответственно 300 м и 100. с. Значение требуемой относительной скорости при этом составит около 3 м/с. В идеальном случае закон управления U(0, управляющий сигнал которого задается в вольтах, для данного случая выглядит, как показано на диаграмме (рис. 13.7), однако действительравными соответственно 300 м и 100. с. Значение требуемой относительной скорости при этом составит около 3 м/с. В идеальном случае закон управления U(0, управляющий сигнал которого задается в вольтах, для данного случая выглядит, как показано на диаграмме (рис. 13.7), однако действительное значение относительного расстояния после автоматического режима реализации этапа ближнего наведения может существенно отличаться от расчетного. Кроме того, следует учитывать возмущения от разности гравитационных ускорений, которые можно оценить лишь приближенно. Отклонения траектории и параметров КА от «опорных» моделируют на основе метода статистических испытаний — таким образом, получают различные «возмущенные» траектории, для которых может быть произведен анализ отклонений относительного расстояния и скорости. Оценку возмущений производят с помощью так называемых «коэффициентов неопределенности», задаваемых в соответствии со степенью уверенности в правильности определения соответствующих величин. В соответствии с теорией нечетких множеств введем (рис. 13.8) нечеткие высказывания по отклонениям параметров движения и действующих возмущений, в частности, по относительному расстоянию (а), относительной скорости (б), возмущению от разности гравитационных ускорений (е) и управлению (г). Следующим шагом после определения вида функций принадлежности, моделирования и фуззификации (приведения к нечеткому виду), является дефуззификация — получение четкого решения. Определенное значение требуемого управления на выходе системы при текущих входных значениях можно получить различными методами, в том числе и тем, который в общем виде описан выше. Однако чаще примспяют цситроидный метод — производят численное интегрирование по всему множеству и поиск «центра масс» под ломаной модульной функцией принадлежности. В рассматриваемом случае был применен альтернативный метод — метод поиска первого максимума. Этот метод обладает удовлетворительной точностью, но требует значительно меньших затрат машинного времени. Результатом расчетов является закон управления для сближения по методу погони в первом приближении. На рис. 13.9 приведена соответствующая зависимость управления U от времени для 406-ти расчетных точек (до точки встречи объектов — активного КА с пассивным). Как следует из полученной зависимости, первоначально действительные параметры отличались от расчетных (опорных), а затем приблизились к ним за счет реализации режимов разгона и торможения КА. 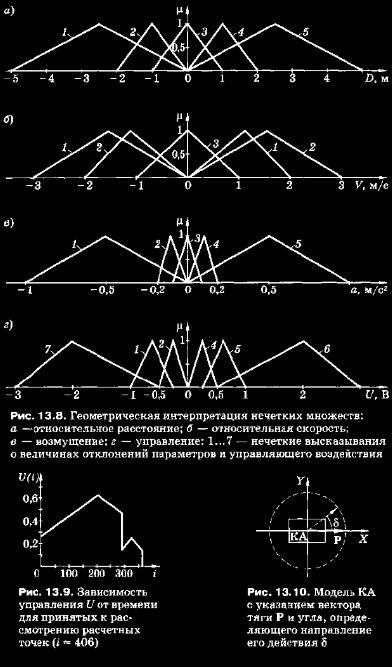 Сравнив полученный результат с приведенным выше «идеальным» законом управления, видим, что система работает адаптивно, подстраиваясь под «возмущенные» начальные условия. Аналогичную ситуацию, с тем различием, что размерность системы увеличивается, наблюдают и в методе параллельного сближения. Соответствия реальной ситуации (уровень адекватности) данной модели достигают выбором функций принадлежности нечетких множеств, отвечающих отклонениям по относительному расстоянию, относительной скорости, возмущению и управлению. В данном случае (см. рис. 13.8) эти функции являются «стандартными» — Z/R-симметричными функциями треугольного вида. Понятно, что в действительности эти функции могут отличаться от стандартных, что делает введенную модель лишь приближенной. МЕТОД АСИМПТОТИЧЕСКОГО ТОРМОЖЕНИЯ. Сущность процесса сближения КА при асимптотическом торможении (методе «затухающего перехвата») заключается [52] в увеличении времени торможения на ближнем участке, предшествующем стыковке, что приводит к уменьшению относительной скорости при сокращении относительного расстояния. Таким образом, встреча происходит при относительной скорости, близкой к нулевой. Необходимость в такой методике сближения возникает вследствие естественного запаздывания в системе и недостаточности тяги управляющих двигателей для выполнения мгновенного торможения при встрече КА. Рассмотрим данный метод для случая компланарного сближения активного КА с базовым пассивным аппаратом, находящимся на круговой орбите. Отметим при этом, что основные принципы управления будут справедливы и для пространственного варианта сближения. При формировании закона управления испольЗуют разность между параметрами опорной и действительной траекторий КА. Разность между расчетным и действительным углами направления вектора тяги (б - бдейств) определяет сигнал рассогласования при формировании закона управления ориентацией вектора тяги Р, формируемого двигательной установкой (ДУ) (рис. 13.10). Для упрощения расчетов потребного времени создания нужного приращения скорости для перехода на траекторйи встречи используем ДУ постоянной тяги. Интервалы времени между приложениями тяги ДУ зависят от наличия ошибки при непрерывном сравнении опорных и текущих действительных величин относительных скоростей. В соответствии с теорией нечетких множеств введем термы соответствующих лингвистических переменных: Отклонение по \х (м/с): положительное большое ................................... 5,0 положительное малое ...................................... 2,0 нулевое .......................................................... 0,5...-0,5 отрицательное малое........................................ 0...-2 отрицательное большое .................................... О...-5 Отклонение по V (м/с): положительное большое ................................... 5...0 положительное малое ...................................... 2...0 нулевое .......................................................... 0,5...-0,5 отрицательное малое........................................ 0...-2 отрицательное большое .................................... 0...-5 Отклонение по U (В): положительное большое ................................... 27...0 нулевое.......................................................... 3...-3 отрицательное малое...................................... —2...-13 отрицательное большое .................................... 0...-27 Геометрическая интерпретация (рис. 13.11) аналогична приведенной выше для метода прямого наведения, т. е. и здесь применяются «стандартные» LR-функции принадлежности треугольного вида. Для иллюстрации решения задачи значения относительного расстояния и времени встречи примем соответственно равными 600 м и 100 с, возмущения на траектории вышеперечисленных контролируемых величин генерируются в рассматриваемой модельной задаче случайным образом.  Кроме традиционного представления структуры синтезированного закона путем «замораживания» одного из входов, после моделирования этой структуры в начальном приближении можно представить отклонения в виде некоторых поверхностей, пример которых для лингвистических переменных «отклонение по Vx* и «отклонение по Vu* приведен на рис. 13.12. Закон управления сближением КА по методу «затухающего перехвата» для данного конкретного случая выглядит так, как показано на рис. 13.13, и адекватен отклонениям контролируемых величин. Сигнал рассогласования {/(£) является сигналом управления углом отклонения вектора тяги Р КДУ КА. В соответствии с методом сближения, при наличии некоторой траектории сближения с пассивным аппаратом, удержание АКА на которой происходит по описанному выше алгоритму, через некоторое время во избежание «жесткой» встречи производят коррекцию этой траектории с учетом более продолжительного времени сближения (путем ввода некоторого фиктивного времени встречи), т. е. вводят новую опорную траекторию. Изменение скорости для каждой последующей траектории будет меньше, чем для предыдущей, и, следовательно, происходит последовательное приближение к нулевой относительной скорости. Параметры новой опорной траектории могут быть также определены нечетко — в зависимости от «резервного» относительного расстояния и текущей относительной скорости. Таким образом получают систему, состоящую из двух подсистем: нечеткой системы управления углом отклонения вектора тяги Р и нечеткой системы формирования параметров последующей опорной траектории. МЕТОД ЭКСПОНЕНЦИАЛЬНОГО УПРАВЛЕНИЯ СБЛИЖЕНИЕМ. Данный метод интересен тем, что управляющие функции формируют в виде линейных комбинаций текущих значений фазовых координат центра масс КА. Рассмотрим случай экспоненциального управления сближением в центральном гравитационном поле. Будем считать, что базовый аппарат находится на известной опорной орбите, и управляющие ускорения АКА во время сближения формируются непрерывно. Относительное движение АКА рассматриваем в орбитальной системе координат OXYZ, центр которой совпадает с центром масс базового аппарата. В этом случае линеаризованные уравнения относительного движения будут иметь вид (13.12). Предположим, что все проекции вектора скорости и ускорения можно определить с достаточно высокой точностью. Также можно с помощью БЦВМ сформировать «опорную» траекторию. В. результате может быть получена достаточная информация для формулирования нечетких правил в нечеткой системе, реализующей закон управления по методу экспоненциального управления сближением. Особенностью данной системы являются три ее выхода, соответствующие проекциям вектора управляющего ускорения на оси принятой к рассмотрению системы координат. С точки зрения математической постановки сближение по данному методу происходит бесконечно долго, но так как КА не является материальной точкой, действительный процесс сближения заканчивается на некотором нулевом расстоянии от начала координат через продолжительный, но ограниченный отрезок времени. Моделируя систему по методике, аналогичной вышеописанной, получим стратегию управления (включающую три закона Ux(t), Uy(t), U2(t), определяющих изменение управляющих ускорений ах,ау, аz) для данного метода. Как показывают исследования, по сравнению с другими методами сближения экспоненциальный метод является более энергетически выгодным, однако при формировании функции принадлежности нечеткой системы управления не всегда удается решить сложную задачу одновременной оптимизации времени сближения и расхода топлива. Рассмотренный анализ применимости теории нечеткого управления для решения задачи сближения КА дает основание считать, что использование обсуждаемого подхода возможно для всех существующих методов сближения. Не исключена также вероятность формирования методов, специально ориентированных на теорию нечеткого управления. Следует также иметь в виду, что использовать вышеизложенную методику непосредственно в прямом виде не представляется возможным, так как несмотря на универсальность и эффективность аппарата нечетких множеств и нечеткой логики в целом, для построенных нечетких систем характерны следующие существенные недостатки: во-первых, исходный набор нечетких правил формулируется оператором нечеткой системы, поэтому он может быть неполным или противоречивым; во-вторых, вид и параметры функций принадлежности, описывающих входные и выходные параметры системы, могут не соответствовать действительности, что также приведет к некорректному решению поставленной задачи. Частичного устранения перечисленных недостатков достигают при применении так называемых адаптивных нечетких систем, корректирующих параметры функции принадлежности. Разновидностью таких систем являются искусственные обучающиеся нечеткие нейронные сети. Ограничившись лишь постановкой задачи и учитывая ее самостоятельное значение, отметим, что нечеткая нейронная сеть по сути является многослойной нейронной сетью с обучением (например, по алгоритму обратного распространения ошибки), причем слои в ней соответствуют этапам функционирования нечеткой системы: первый слой выполняет функцию фуззифика-ции на основе заданных оператором в первом приближении функций принадлежности; второй слой является совокупностью нечетких правил; третий слой выполняет функцию дефуззификации, т. е. приведения к четкости (значение г). Пример подобной гибридной системы (в сопоставлении с блок-схемой нечеткого контроллера), для которой входами являются некоторые величины х1 и х2, приведен на рис. 13.14, где блоки Ф реализуют функцию фуззификации, блок Д — дефуззификации, блоки логического сложения реализуют принятую к рассмотрению совокупность нечетких правил. Приведенное к четкости значение г, в частности, может иметь физический смысл искомого коэффициента (матрицы коэффициентов) усиления контура управления k. 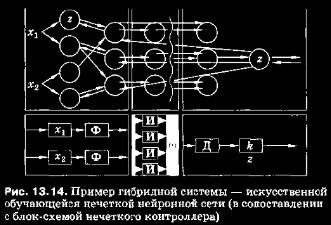 Процесс обучения нечеткой обучающейся нейронной сети заключается в сопоставлении оператором входных значений (отклонений от опорных значений или от усредненных величин возмущений) и оптимальных значений управления (на основе накопленного опыта), что в итоге приводит к формированию скорректированных функций принадлежности. в результате значение управления на выходе сети будет оптимальным, а роль некоторого функционала J (критерия оптимальности, например, сред неинтегральной абсолютной ошибки) и оптимальных коэффициентов уточнения «нечетких высказываний» выполняют веса и смещения синапсов первого слоя нейронной сети, корректирующих функции принадлежности. Нечеткий контроллер, построенный по подобного рода обученной системе, в состоянии в определенном смысле оптимально и надежно формировать адекватные сигналы управления, в том числе и при выполнении задачи сближения КА в условиях неопределенности, например, в случае проведения спасательных работ, связанных с возникновением нештатной ситуации на орбите. |
Статьи:
Видео:
Последние новости:
| Терраформирование Венеры |
| Эктазийский период |
| Юпитер, Ио и его тень |
| Небесные тела на Земле. Часть 2 |
| Новый солнечный цикл уже начался? |
Видео:
 | Kepler Co-Investigator Natalie Batalha |
 | НЛО вторжение на землю (6/6) |
 | Путешествие на край Вселенной. часть 9/10 |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2024 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


