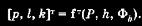11.7. Аналитическое определение корректирующих воздействий при различных составах управляемых параметров
При рассмотрении корректирующего маневра как процесса управления возникает необходимость определения взаимосвязи корректирующих воздействий с управляемыми параметрами. Отчасти результатом решения соответствующей задачи могли бы служить материалы, изложенные в § 10.3. Дело в том, что при любой математической постановке задачи коррекции во главу угла ставится условие достижения близости реализуемого и номинального движений. Поэтому и с точки зрения выбираемых критериев качества, и с точки зрения используемой модели движения приоритет должен быть отдан «точностным» построениям, физически гарантирующим более высокую, чем при выполнении маневра орбитального перехода, точность процесса.
Имея это в виду, в качестве подлежащего минимизации критерия, в отличие от (10.34), здесь уже более целесообразным является использование критерия вида
Изложенная в § 10.3 методика, базирующаяся на стандартной процедуре линеаризации модели, оказывается здесь неприемлемой в силу грубости допущения о линейной зависимости корректируемых параметров от корректирующих импульсов скорости.
Для повышения точности линеаризованных моделей может быть рекомендована методика, полное изложение которой приведено в [16]. Здесь же ограничимся рассмотрением общей идеи, положенной в ее основу.
Методика основана на предположении существования взаимнооднозначного преобразования вида
В последнем случае из множества возможных решений выбирают такое, которое доставляет минимум суммарному приращению корректирующей скорости, т. е. задачу сводят к оптимизационной по критерию (10.34) при удовлетворении ограничений типа равенств, заданных уравнениями (11.37) и (11.42). Естественно, что при этом в зависимости от выбранного варианта проведения коррекции меняется и состав ограничений.
Далее рассмотрим достаточно простой двухимиульсный маневр коррекции орбиты, тем не менее сохраняющий основные элементы общего решения. Покажем алгоритмическую схему решения задач, имеющую цель получения орбиты с заданными значениями периода обращения Р, минимальной высоты орбиты над поверхностью Земли h и географической широты, соответствующей минимальной высоте Фh.
Итак, предположим, что существует однозначная зависимость
Тогда вместо зависимостей параметров управления от P, h, Фk можно записать уравнения относительно р, I, k типа (11.37) и (11.42). Таким образом, математическая модель для определения начального приближения параметров управления будет включать в себя функционал вида (10.34) и ограничения типа равенств в форме (10.45).
Применяя упоминавшийся ранее метод множителей Лагран-жа, можно, составив функцию Лагранжа и приравняв нулю производные этой функции по параметрам управления, получить систему уравнений, решение которой позволит найти оптимальные по энергетике параметры управления.
Подобным же образом находят решение и при ином составе корректируемых элементов орбиты.В случае же неполного состава корректируемых элементов задача может быть сведена [16] к рассматриваемой путем расширения корректируемых элементов до полного и добавления соответствующих уравнений в линеаризованную модель уравнений корректирующего маневра.
|