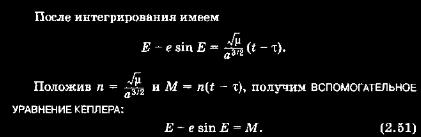2.10. Эллиптическое движение
Вычислив интеграл (2.47), мы можем получить (t - т) как функцию u (и наоборот). Но этот прямой путь оказывается чрезвычайно сложным, так как требует решения трансцендентного уравнения, которое в конечном виде не решается. К некоторому упрощению ведет использование другой вспомогательной переменной, через которую u выражается достаточно просто, а связь со временем определяют более простым трансцендентным уравнением.
В эллиптическом движении вводят понятие эксцентрической аномалии E:
После интегрирования имеем
Уравнение (2.51) в конечном виде решают только в некоторых частных случаях. Как правило, пользуются специальными таблицами или решение (2.51) осуществляют методом последовательных приближений.
Рассмотрим смысл введенных понятий Е, n, М.
На рис. 2.3 показана взаимосвязь истинной д и эксцентрической Е аномалий. На большой оси эллипса строят круг радиуса а. Из точки т, определяющей положение КА на эллиптической орбите, восставляют перпендикуляр к большой полуоси, который продлевают до пересечения с окружностью, и из точки пересечения проводят радиус-вектор в центр О. Пусть движение начинается из перицентра, т. е. т = 0. Тогда время полного оборота по орбите даст нам период обращения Г*. Итак, 360° = пТ или п - 360°/Т — средняя угловая скорость движения КА или среднее движение. Величину М называют Средней аномалией. Действительно, М возрастает пропорционально времени и равно нулю при t = т, т. е. когда КА находится в перицентре (u = Е = 0). При t = х + (в апоцентре) М = 180° (u = Е = М). В конце полного оборота М - 360' (u - Е - М).
* Кроме указанного обозначения периода обращения в ряде источников, так же как и в данном издании, используют обозначение Р, поскольку Т принято также обозначать трансверсальную составляющую ускорения.
|