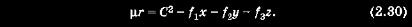2.7. Переход к орбитальным координатам
Приведенные соотношения свидетельствуют о том, что общее решение дифференциальных уравнений невозмущенного движения существует. А как их решить практически?
Действительно, чтобы получить формулы (2.21), нужно разрешить уравнения (2.7)...(2.9), (2.13) и (2.17) относительно пяти из шести неизвестных функций. Но эти уравнения являются уравнениями 2-й степени относительно всех шести неизвестных и содержат иррациональность, представляемую радиусом-вектором. Поэтому непосредственное использование найденных соотношений затруднительно. К некоторому упрощению приводит использование выявленных ранее некоторых свойств. Как было показано при анализе соотношения (2.12), траектория КА является плоской кривой. Чтобы определить вид и расположение этой кривой, надо иметь второе уравнение, содержащее координаты КА; его находят из интегралов Лапласа. Оно имеет вид
Уравнение (2.30) содержит только координаты движущегося КА и представляет собой уравнение некоторой поверхности (поверхности вращения), на которой КА остается в процессе движения. В силу этого, уравнения (2.12) и (2.30) определяют общие уравнения траектории движения КА, которая представляет собой линию пересечения плоскости (2.12) и поверхности 2-го порядка (2.30). Эта линия пересечения является кривой второго порядка. В результате орбита КА при невозмущенном движении представляет собой коническое сечение, которое может быть окружностью, эллипсом, параболой, гиперболой или парой прямых линий (в вырожденном случае).
Невозмущенная орбита — плоская кривая 2-го порядка, один из фокусов которой находится в начале координат (в притягивающем центре), а главная ось совпадает с направлением вектора Лапласа. Ось орбиты в астрономии и космической баллистике называют линией апсид. Ближайшую точку к притягивающему центру называют перицентром (перигеем — для Земли), а наиболее удаленную апоцентром (апогеем).
|