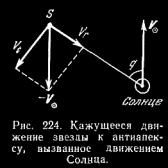
§ 165. Пространственные скорости звезд и движение Солнечной системы
Если известно собственное движение звезды m в секундах дуги за год (см. § 91) и расстояние до нее r в парсеках, то не трудно вычислить проекцию пространственной скорости звезды на картинную плоскость. Эта проекция называется тангенциальной скоростью Vt и вычисляется по формуле
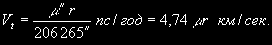 (12.3) (12.3)
Чтобы найти пространственную скорость V звезды, необхо димо знать ее лучевую скорость Vr , которая определяется по доплеровскому смещению линий в спектре звезды (§ 107). По скольку Vr и Vt взаимно перпендикулярны, пространственная скорость звезды равна
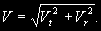 (12.4) (12.4)
Знание собственных движений и лучевых скоростей звезд позволяет судить о движениях звезд относительно Солнца, ко торое вместе с окружающими его планетами также движется в пространстве. Поэтому наблюдаемые движения звезд складываются из двух частей, из которых одна является следствием движения Солнца, а другая — индивидуальным движением звезды.
Чтобы судить о движениях звезд, следует найти скорость движения Солнца и исключить ее из наблюдае мых скоростей движения звезд.
Определим величину и направле ние скорости Солнца в пространстве. Та точка на небесной сфере, к кото рой направлен вектор скорости Солнца, называется солнечнымапексом, а противоположная ей точка — антиапексом. Чтобы пояснить прин цип, на основании которого находят положение солнечного апек са, предположим, что все звезды, кроме Солнца, неподвижны. В этом случае наблюдаемые собственные движения и лучевые скорости звезд будут вызваны только перемещением Солнца, происходящим со скоростью V¤ (рис. 224). Рассмотрим какую-нибудь звезду S, направление на которую составляет угол q с вектором V¤. Поскольку мы предположили, что все звезды не подвижны, то кажущееся относительно Солнца движение звез ды S должно иметь скорость, равную по величине и противопо ложную по направлению скорости Солнца, т.е. — V¤. Эта ка жущаяся скорость имеет две составляющие: одну — вдоль луча зрения, соответствующую лучевой скорости звезды
Vr = V¤cos q,(12.5)
и другую, — лежащую в картинной плоскости, соответствующую собственному движению звезды,
Vt = V¤ sin q.(12.6)
Учитывая зависимость величины этих проекций от угла q, получим, что вследствие движения Солнца в пространстве лу чевые скорости всех звезд, находящихся в направлении движе ния Солнца, должны казаться меньше действительных на величину V¤. У звезд, находящихся в противоположном направле нии, наоборот, скорости должны казаться больше на ту же ве личину. Лучевые скорости звезд, находящихся в направлении, перпендикулярном к направлению движения Солнца, не изме няются. Зато у них будут собственные движения, направленные к антиапексу и по величине равные углу, под которым с рас стояния звезды виден вектор V¤. По мере приближения к апек су и антиапексу величина этого собственного движения умень шается пропорционально sin q, вплоть до нуля.
В целом создается впечатление, что все звезды как бы убе гают в направлении к антиапексу.
Таким образом, в случае, когда движется только Солнце, величину и направление скорости его движения можно найти двумя способами: 1) измерив лучевые скорости звезд, находящихся в разных направлениях, найти то направление, где лучевая скорость имеет наибольшее отрицательное значение; в этом направлении и находится апекс; скорость движения Солн ца в направлении апекса равна найденной максимальной луче вой скорости; 2) измерив собственные движения звезд, найти на небесной сфере общую точку, к которой все они направлены: противоположная ей точка будет апексом; для определения величины скорости Солнца надо сначала перевести угловое пе ремещение в линейную скорость, для чего необходимо выбрать звезду с известным расстоянием, а затем найти V¤ по формуле (12.6).
Если теперь допустить, что не только Солнце, но и все дру гие звезды имеют индивидуальные движения, то задача услож нится. Однако, рассматривая в данной области неба большое количество звезд, можно считать, что в среднем индивидуаль ные их движения должны скомпенсировать друг друга. Поэтому средние значения собственных движений и лучевых скоростей для большого числа звезд должны обнаруживать те же законо мерности, что и отдельные звезды в только что рассмотренном случае движения одного только Солнца.
Описанным методом установлено, что апекс Солнечной си стемы находится в созвездии Геркулеса и имеет прямое вос хождение a = 270° и склонение d = +30°. В этом направлении Солнце движется со скоростью около 20 км/сек.
|
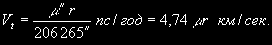 (12.3)
(12.3)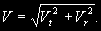 (12.4)
(12.4)