Курс общей астрономии
|
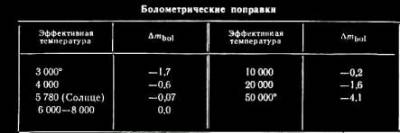
§ 147. Абсолютная звездная величина и светимость звезд Видимые звездные величины ничего не говорят ни об общей энергии, излучаемой звездой, ни о яркости ее поверхности. Действительно, вследствие различия в расстояниях маленькая, сравнительно холодная звезда только из-за своей относительно большой близости к нам может иметь значительно меньшую видимую звездную величину (т.е. казаться ярче), чем далекий горячий гигант. Если расстояния до двух звезд известны (см. § 63), то на основании их видимых звездных величин легко найти отношение излучаемых ими действительных световых потоков. Для этого достаточно освещенности, создаваемые этими звездами, отнести к общему для всех звезд стандартному расстоянию. В качестве такого расстояния принимается 10 пс. Звездная величина, которую имела бы звезда, если ее наблюдать с расстояния в 10 пс, называется абсолютной звездной величиной. Как и видимые, абсолютные звездные величины могут быть визуальными, фотографическими и т.д. Пусть видимая звездная величина некоторой звезды равна m, а расстояние ее от наблюдателя составляет r пс. По определению, звездная величина с расстояния 10 пс будет раина абсолютной звездной величине М. Применяя к m и М формулу (7.8), получим 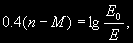 (11.2) (11.2)где Е и Е0 — соответственно освещенности от звезды с расстояния r пс и 10 пс. Поскольку освещенности обратно пропорциональны квадратам расстояний, то 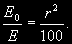 (11.3) (11.3)Подставляя (11.3) в (11.2), получим 0,4(m — M) = 2 lg r — 2(11.4) или M = m + 5 — 5 lg r.(11.5) Формула (11.5) позволяет найти абсолютную звездную величину М, если известна видимая звездная величина объекта m и расстояние до него r, выраженное в парсеках. Если же абсолютная звездная величина известна из каких-нибудь других соображений, то, зная видимую звездную величину, легко найти выраженное в парсеках расстояние из условия lg r = 1 + 0,2 (m — M).(11.6) Величина (m — М) называется модулем расстояния. Так как годичный параллакс p светила и расстояние r до него в парсеках связаны соотношением r = 1/p (см. § 63), то формулу (11.6) можно привести к другому виду: M = m + 5 + 5 1g p.(11.7) В качестве примера найдем абсолютную визуальную звездную величину Солнца, видимая визуальная звездная величина которого т¤ = —26m,8 (см. § 103). Расстояние до Солнца 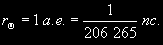 Подставляя m¤ и lg r¤ в формулу (11.5), получаем Подставляя m¤ и lg r¤ в формулу (11.5), получаем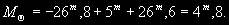 При определении звездной величины (например, визуальной) непосредственно из наблюдений регистрируется только та часть излучения, которая прошла сквозь земную атмосферу, данную оптическую систему и зарегистрирована светочувствительным прибором. Чтобы найти суммарное излучение во всем спектре, необходимо к результатам этих измерений прибавить поправку, Учитывающую излучение, не дошедшее до прибора. Звездная величина, определенная с учетом излучения во всех участках спектра, называется болометрической. Разность между болометрической звездной величиной и визуальной или фотовизуальной называется болометрической поправкой 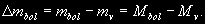 (11.8) (11.8)Болометрические поправки вычисляются теоретически. В самое последнее время для этой цели привлекаются результаты внеатмосферных измерений излучения звезд в ультрафиолетовой области спектра. Болометрическая поправка имеет минимальное значение для тех звезд, которые в видимой области спектра излучают наибольшую долю всей своей энергии, и зависит от эффективной температуры звезды (табл. 10). Болометрические поправки позволяют определить болометрические светимости тех звезд, для которых известны абсолютные визуальные звездные величины. Пусть Mv — абсолютная визуальная звездная величина некоторой звезды, а Dmbol — болометрическая поправка. Тогда болометрическая абсолютная величина звезды 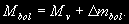 (11.9) (11.9)Применим эту формулу к Солнцу, болометрическую поправку для которого примем, округляя значение из табл. 10: 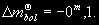 Так как абсолютная визуальная звездная величина Солнца 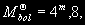 его болометрическая абсолютная звездная величина его болометрическая абсолютная звездная величина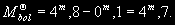 Поток энергии излучаемой звездой по всем направлениям, называется светимостью. Между светимостями L и абсолютными звездными величинами должно выполняться то же соотношение, что и между Е и m в формуле (7.8). Поэтому если обозначить величины, относящиеся к Солнцу и к какой-либо звезде, соответственно значками ¤ и *, то получим 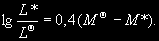 (11.10) (11.10)Обычно светимость выражают в единицах светимости Солнца, т.e. L¤ = 1 и 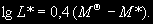 (11.11) (11.11)В зависимости от метода определения звездных величин, входящих в эту формулу, получаем визуальные, фотографические или болометрические светимости. Для болометрических светимостей, подставляя значение 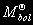 и учитывая (11.9), имеем и учитывая (11.9), имеем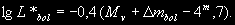 (11.12) (11.12)
|
Статьи:
Видео:
Последние новости:
| Аскреус |
| Солнечный удар по энергосистемам |
| Расширяющаяся вселенная |
| В сердце Краба |
| Темная материя гравитационной линзы |
Видео:
 | НЛО - Факты и Мистификации 1-5 |
 | НЛО вторжение на землю (1/6) |
 | Три цвета Вселенной |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|