Курс общей астрономии
|
§ 41. Элементы орбит планет. Основные задачи теоретической астрономии Движение планеты будет вполне определено, если известны плоскость, в которой лежит ее орбита, размеры и форма этой орбиты, ее ориентировка в плоскости и, наконец, момент времени, в который планета находится в определенной точке орбиты. Величины, определяющие орбиты планеты, называются элементами ее орбиты. За основную плоскость, относительно которой определяется положение орбиты, принимается плоскость эклиптики. Две точки, в которых орбита планеты пересекается с плоскостью эклиптики, называются узлами — восходящим и нисходящим. Восходящий узел тот, в котором планета пересекает эклиптику, удаляясь от ее южного полюса. Эллиптическую орбиту планеты определяют следующие 6 элементов (рис. 28): 1. Наклонение i плоскости орбиты к плоскости эклиптики. Наклонение может иметь любые значения между 0 и 180°. Если 0 £ i < 90°, то планета движется вокруг Солнца (С) в том же направлении, что и Земля (прямое движение); если 90° < i < 180°, то планета движется в противоположном направлении (обратное движение). 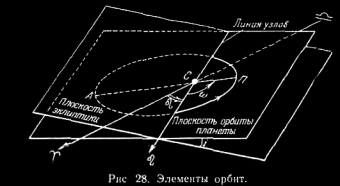 2. Долгота (гелиоцентрическая) восходящего узла <, т.е. угол между направлениями из центра Солнца на восходящий узел и на точку весеннего равноденствия. Долгота восходящего узла может иметь любые значения от 0 до 360°. Долгота восходящего узла < и наклонение i определяют положение плоскости орбиты в пространстве. 3. Угловое расстояние w перигелия от узла, т.е. угол между направлениями из центра Солнца на восходящий узел <, и на перигелий П. Он отсчитывается в плоскости орбиты планеты в направлении ее движения и может иметь любые значения от 0 до 360°. Угловое расстояние перигелия w определяет положение орбиты в ее плоскости. (Иногда вместо w дается долгота перигелия p = < + w) 4. Большая полуось а эллиптической орбиты, которая однозначно определяет сидерический период обращения Т планеты. Часто одновременно с ней дается в качестве элементасреднее суточное движение п = 360° / T = 2p / T, т.е. средняя угловая скорость планеты за сутки. 5. Эксцентриситет орбиты 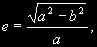 где а и b — полуоси эллиптической орбиты. где а и b — полуоси эллиптической орбиты.Большая полуось а и эксцентриситет е определяют размеры и форму орбиты. 6. Момент прохождения через перигелий t0 , или положение планеты на орбите в какой-нибудь определенный момент времени t (долгота в эпоху t). Зная момент прохождения через перигелий t0 и другие элементы орбиты, можно определить положение планеты в плоскости ее орбиты для любого момента времени t.  Положение планеты на орбите определяется двумя величинами: радиусом-вектором r и истинной аномалией q. Истинной аномалией планеты называется угол ПСР (рис. 29) между направлением из Солнца (С) на перигелий П и радиусом-вектором планеты Р. Радиус-вектор r и истинная аномалия q вычисляются по формулам r = a (1 — e cos E),(2.9) 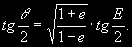 (2.10) (2.10)где Е = Ð ПON и называется эксцентрической аномалией. Эксцентрическая аномалия Е вычисляется из уравнения Кеплера M = E — e sin E,(2.11) где М — угол, называемый средней аномалией. Средняя аномалия представляет собой дугу круга, которую описала бы планета за время (t—t0), если бы она двигалась равномерно по окружности радиуса а со средней угловой скоростью п, т.е. 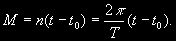 (2.12) (2.12) Вычисление положения планеты на орбите для некоторого момента времени t проводится в следующей последовательности: 1) по формуле (2.12), в которой известны Т и (t — t0), определяют среднюю аномалию М; 2) по формуле (2.11), при известных е и М, методом последовательных приближений находят эксцентрическую аномалию Е; 3) по формулам (2.9) и (2.10) вычисляют радиус-вектор r и истинную аномалию q . Определив положение планеты на орбите для заданных моментов времени, можно вычислить для этих же моментов ее пространственные гелиоцентрические координаты. Зная же элементы орбиты Земли и вычислив для тех же моментов положение Земли на ее орбите, можно определить геоцентрические координаты планеты и найти ее расстояние от центра Земли. Определение видимых координат планеты по элементам их орбит называется вычислением эфемерид, т.е. таблиц, в которых положения планет даются на любые избранные моменты времени (иногда на много лет вперед). Обратная задача, т.е. определение элементов орбит по наблюденным координатам, называется определением орбит. Эта задача гораздо труднее вычисления эфемерид. Кеплер решил ее для тех планет, которые наблюдаются уже давно. Методы же определения орбит по нескольким (не менее 3-х) наблюдениям, что особенно важно при открытии новых планет и комет, были разработаны лишь в начале XIX в. Вычисление эфемерид и определение орбит — основные задачи теоретической астрономии. |
Статьи:
Видео:
Последние новости:
| Фотосфера |
| Образование галактик |
| Обреченная звезда Eta Carinae |
| Внеземная жизнь. Опыт первый. |
| Вселенные рождались не однажды |
Видео:
 | Astronauts Overcome Obstacles to Upgrade Hubble |
 | Kepler Arrival |
 | Путешествие сквозь космос |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


