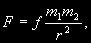§ 43. Закон всемирного тяготения Ньютона
Основные законы движения тел позволили Ньютону сформулировать и математически доказать следующую теорему: "Силы, которыми главные планеты постоянно отклоняются от прямолинейного движения и удерживаются на своих орбитах, направлены к Солнцу и обратно пропорциональны квадратам расстояния от его центра”.
Доказав далее, что сила, удерживающая планеты на их орбитах, тождественна с силой тяжести, действующей на поверхности Земли, Ньютон обобщил эту теорему и выразил ее в форме закона всемирного тяготения:
"Каждые две частицы материи притягивают взаимно друг друга, или тяготеют друг к другу, с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними”.
Математически закон всемирного тяготения Ньютона записывается так:
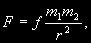 (2.16) (2.16)
где m1 и m2 — массы частиц, r — расстояние между ними, f — коэффициент пропорциональности, равный силе, с которой притягиваются друг к другу две частицы с единичными массами и находящиеся на единичном расстоянии друг от друга.
Коэффициент f называется постоянной тяготения, или гравитационной постоянной.
В системе CGS (сантиметр, грамм, секунда)
f = 6,67 · 10 -8 см3 / г · сек2
Следовательно, две материальные частицы, с массами по 1 г каждая и находящиеся на расстоянии 1 см одна от другой, притягиваются друг к другу с силой в 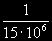 дины. дины.
В астрономии расстояния между Солнцем и планетами часто выражают в астрономических единицах (а.е.), массы небесных тел в массах Солнца, а время — в средних солнечных сутках. В этой системе единиц, называемой гауссовой, постоянная тяготения f = k2 = 0,00029591, а величина k = 0,0172021 » 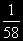 называется гауссовой постоянной. , но только обратно направленное, т.е. называется гауссовой постоянной. , но только обратно направленное, т.е.
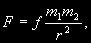
или
F2 = — F1 .
|
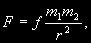 (2.16)
(2.16)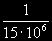 дины.
дины.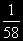 называется гауссовой постоянной. , но только обратно направленное, т.е.
называется гауссовой постоянной. , но только обратно направленное, т.е.