Курс общей астрономии
|
§ 10. Небесная сфера При изучении видимых движений небесных тел необходимо с той или иной степенью точности определять их положения в моменты наблюдений. При этом нет необходимости знать расстояния до них, поскольку все тела представляются нам как бы находящимися на внутренней поверхности некоторой сферы произвольного радиуса. Поэтому видимые, положения светил можно определять только направлениями, а их взаимное расположение — углами между этими направлениями, или соответствующими дугами больших кругов на сфере, из центра которой исходят все направления. Воображаемая сфера произвольного радиуса с центром в произвольной точке пространства, на поверхности которой расположены светила так, как они видны на небе в некоторый момент времени из дачной точки пространства, называется небесной сферой. Таким образом, воображаемый наблюдатель, находящийся в центре небесной сферы, должен видеть положения светил на ее поверхности точно в таком же взаимном расположении, в каком реальный наблюдатель видит реальные светила на небе. Вращение небесной сферы повторяет вращение небесного свода. Небесная сфера служит для изучения видимых положений и движений небесных тел. Для этого на ее поверхности фиксируются основные линии и точки, по отношению к которым и производятся соответствующие измерения. 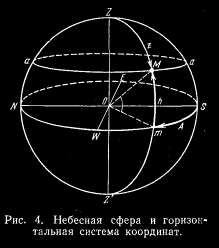 Прямая ZOZ' (рис. 4), проходящая через центр О небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения, называется отвесной или вертикальной линией. Отвесная линия пересекается с поверхностью небесной сферы в двух точках: в зените Z, над головой наблюдателя, и в диаметрально противоположной точке — надире Z'. Большой круг небесной сферы (SWNE), плоскость которого перпендикулярна к отвесной линии, называется математическим или истинным горизонтом. Математический горизонт делит поверхность небесной сферы на две половины: видимую для наблюдателя, с вершиной в зените Z, и невидимую, с вершиной в надире Z'. Математический горизонт следует отличать от видимого горизонта (линии, вдоль которой «небо сходится с Землей»). Видимый горизонт на суше — неправильная линия, точки которой лежат то выше, то ниже истинного горизонта. В открытом море видимый горизонт всегда малый круг, плоскость которого параллельна плоскости математического горизонта. Малый круг небесной сферы (аМа), проходящий через светило М и плоскость которого параллельна плоскости математического горизонта, называется альмукантаратомсветила. Большой полукруг небесной сферы ZMZ', проходящий через зенит, светило М и надир, называется кругом высоты, вертикальным кругом, или просто вертикалом светила. 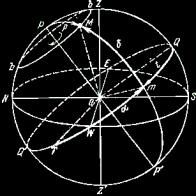 Рис. 5. Небесная сфера и экваториальные системы координат. Диаметр РР' (рис. 5) вокруг которого происходит вращение небесной сферы, называется осью мира. Ось мира пересекается с поверхностью небесной сферы в двух точках: в северном полюсе мира Р и южном полюсе мира Р'. Северный полюс тот, со стороны которого вращение небесной сферы происходит по часовой стрелке, если смотреть на сферу извне. Большой круг небесной сферы QWQ'E, плоскость которого перпендикулярна к оси мира, называется небесным экватором. Небесный экватор делит поверхность небесной сферы на два полушария: северное, с северным полюсом мира Р, и южное, с южным полюсом мира Р'. Малый круг небесной сферы (bМb), плоскость которого параллельна плоскости небесного экватора, называется небесной или суточной параллелью светила М. Видимые суточные движения светил совершаются по суточным параллелям. Большой полукруг небесной сферы РМР', проходящий через полюсы мира и через светило М, называется часовым кругом или кругом склонения светила. Небесный экватор пересекается с математическим горизонтом в двух точках: в точке востока Е и в точке запада W. Круги высот, проходящие через точки востока и запада, называются первыми вертикалами — восточным и западным. Большой круг небесной сферы PZQSP'Z'Q'N, плоскость которого проходит через отвесную линию и ось мира, называется небесным меридианом. Небесный меридиан делит поверхность небесной сферы на два полушария: восточное, с точкой востока Е, и западное, с точкой запада W. Плоскость небесного меридиана и плоскость математического горизонта пересекаются по прямой линии NOS, которая называется полуденной линией. Небесный меридиан пересекается с математическим горизонтом в двух точках: в точке севера N и в точке юга S. Точкой севера называется та, которая ближе к северному полюсу мира. Точка юга — ближе к южному полюсу мира. Небесный меридиан пересекается с небесным экватором также в двух точках: в верхней точке экватора Q, которая ближе к зениту, и в нижней точке экватора Q', которая ближе к надиру. Дуга небесного меридиана PZQSP' является его верхней частью, а дуга PNQ'Z'P' — нижней. |
Статьи:
Видео:
Последние новости:
| Рентгеновское излучение Сириуса B |
| NGC 1850: газовые облака и звездные скопления |
| Тысячелетие изучения Земли |
| Venus Express подтвердил наличие двойного вихря на южном полюсе Венеры |
| 22 мили от Эроса |
Видео:
 | НЛО вторжение на землю (2/6) |
 | Описание черных дыр |
 | Нибиру на ОРТ |
Последние новости:
| Зонд НАСА рассмотрел ледяные горы на поверхности Плутона |
| На Землю надвигается сильный метеоритный дождь |
| NASA создаст роботов для ремонта и дозаправки спутников |
| Россия и Япония совместно построят космический телескоп |
|
WalkInSpace.Ru Правила: «Путешествие в космос» © 2025 Использование материалов допускается при условии указания авторства WalkInSpace.ru и активной ссылки на www.WalkInSpace.ru. |
|


